In September 2015 the twin advanced detectors of the Laser Interferometer Gravitational-Wave Observatory (LIGO) made the first ever direct detection of gravitational waves from the merger of two massive black holes more than a billion light years away. This discovery event, known as GW150914, came one hundred years after the prediction of gravitational waves by Albert Einstein’s General Theory of Relativity. It was followed by another candidate event (known as LVT151012) in October 2015 and then a second confirmed detection (known as GW151226) in December 2015 – again involving the merger of a pair of black holes.
Advanced LIGO began its second Observing Run in late November 2016, after upgrades designed to further enhance the detectors’ remarkable sensitivity. About one month later a third confirmed detection of gravitational waves was made, known as GW170104. In this article we summarise how GW170104 was detected, what we have learned about the black holes that produced it, and how this new LIGO discovery improves our understanding of the nature of gravity and spacetime.
Detection of the GW170104 signal
GW170104 was observed by the advanced LIGO detectors in Hanford Washington and Livingston Louisiana. Thorough investigations of the detectors’ status at the time, similar to those carried out for the previous detections (see here and here), revealed that both detectors were operating normally.
The top two panels of Figure 1 show the data measured by the two LIGO instruments at the time of the merger. The GW170104 signal closely resembles that of GW150914: in both cases the LIGO data clearly display the characteristic “chirp” pattern expected for the gravitational waves emitted from the merger of two black holes – i.e. a sharp upward sweep in amplitude and frequency as they orbit each other ever faster before they merge.
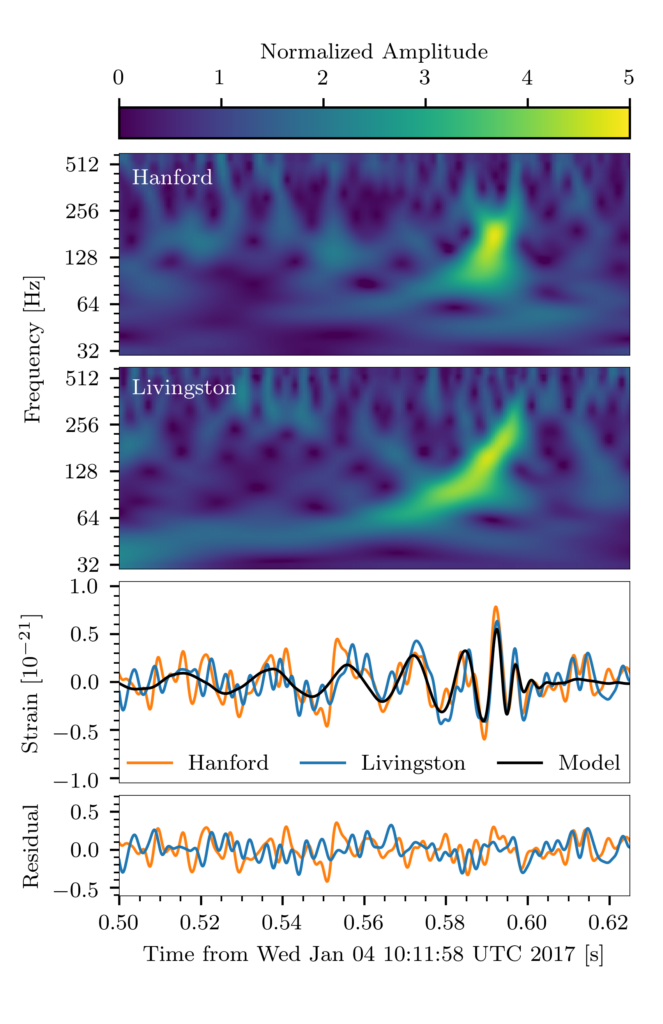
Figure 1. The upper two panels show a plot of the frequency evolution of the signal measured by each of the Advanced LIGO detectors, over a roughly 0.1 second interval, around the time of the detection of GW170104. The strength, or amplitude, of the signal is represented by the color bar. The third panel compares the best-fitting gravitational waveform model (shown in black) for the black hole merger with the gravitational-wave strain data measured by both LIGO detectors. The data have been adjusted for the 3-millisecond difference in arrival time of the signal at the Hanford and Livingston detectors, and for the different orientation of the detectors’ interferometer arms. The lowest panel shows the difference between these data and the best-fit model; we can see that the difference shows no obvious pattern.
Using a technique known as matched filtering (see also here and here), the GW170104 data were compared to a bank of theoretical waveforms, to find the best match and extract some physical properties of the candidate source — such as its constituent masses and its sky position. Rough estimates of these properties were sent very quickly to our astronomer partners around the world so they might look for “electromagnetic counterparts” – emission in the form of light that might be associated with the gravitational-wave event. (You can read more here about the searches for an associated electromagnetic counterpart of GW150914).
Determining the properties of GW170104
A more thorough matched filtering analysis of the data was then carried out over several weeks, using powerful supercomputers. The goal of this analysis was first to determine the significance of the detection by calculating a false alarm rate for the event — i.e. how often could we expect to see a signal similar to GW170104 simultaneously in both detectors, purely as a result of coincident features in the detectors’ background “noise”? The lower the false alarm rate, the smaller the chance that GW170104 was an artefact of the instruments; more details about how the false alarm rate is calculated for LIGO data can be found here and here).
Our analysis computed a false alarm rate of less than once every 70,000 years – rare enough to indicate that GW170104 was indeed a highly significant detection of a real, astrophysical event!
The third panel of Figure 1 shows a comparison between the best-fitting waveform model and the time series data (expressed as gravitational-wave strain, equal to the fractional change in the distance between two measurement points as a gravitational wave passes by) observed by the LIGO detectors at the time of the GW170104 merger event. The lowest panel shows the difference between these data and the best-fitting model; we can see that the best-fit model gives a good match to the data.
Further supercomputer analysis then allowed us to extract more precise estimates of the parameters of GW170104 – i.e. the physical properties of the event, including the masses of the merging compact objects, their distance from the Earth and position on the sky, the orientation of their orbital plane and constraints on the rate at which they are spinning and their orbit is precessing. The process of parameter estimation involves carefully checking millions of combinations of these model characteristics and testing how well the gravitational waveform predicted for each set of parameters matches the signal measured by the LIGO detectors. (See also here and here, for more information about how gravitational-wave parameter estimation is carried out).
We can estimate the uncertainty on the GW170104 model parameters – both individually and in combinations. As an example, Figure 2 shows what we can infer about the masses of the two compact objects, which we found to be about 30 times and 20 times the mass of the Sun respectively, indicating that GW170104 was the merger of a pair of black holes. From the estimated mass of the final black hole we found that the energy of about two times the mass of the Sun was radiated in the form of gravitational waves during the merger event. This corresponds to a peak gravitational-wave luminosity that was briefly many times larger than the combined light power of every star in the entire observable Universe!
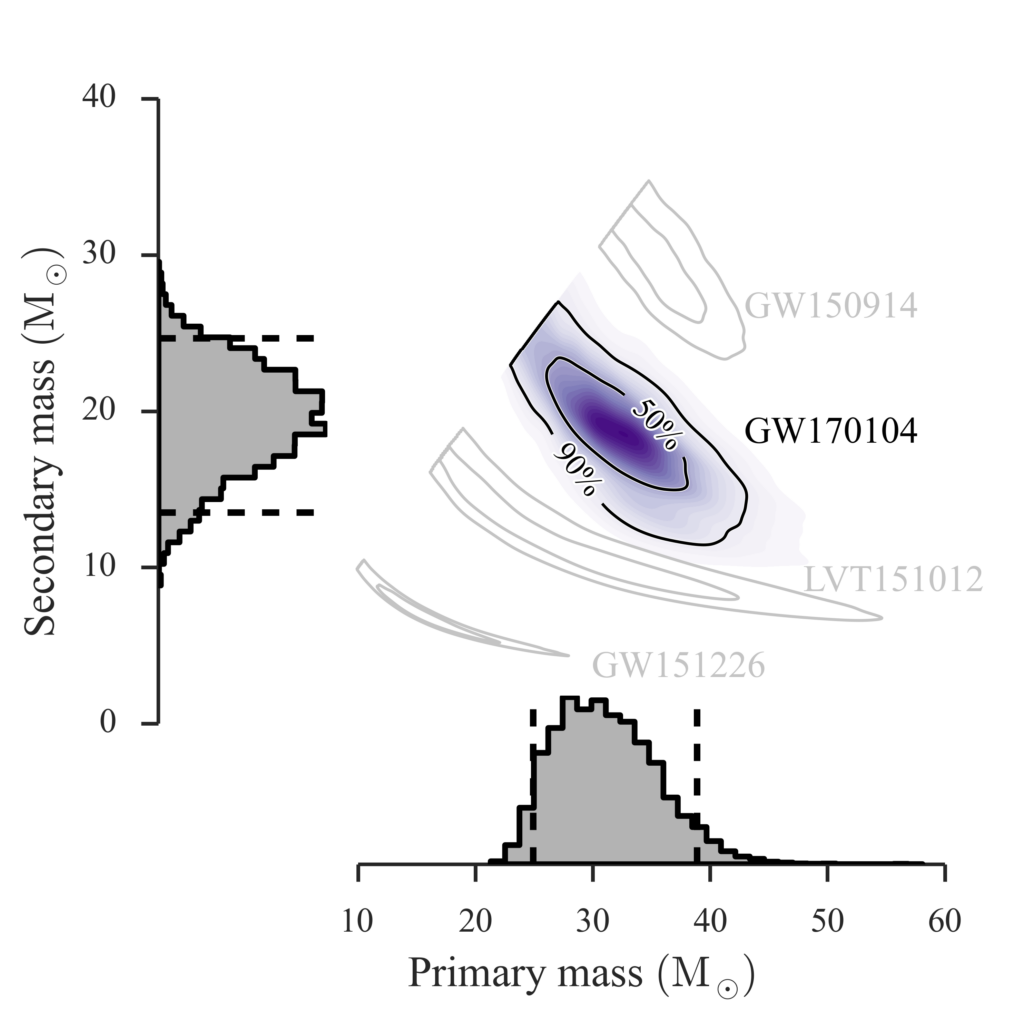
Figure 2. This image shows the range of black hole masses, in units of the mass of the Sun, consistent with the GW170104 signal. The contour map in the upper right part of the figure shows which combinations of black hole masses are consistent, for the two black holes considered together. Regions where the contour map is darker show mass combinations that have higher probability of being correct. The grey ‘hills’ (known as histograms) show the relative probability of different masses for each black hole considered separately, and peak at about 30 and 20 solar masses respectively. Probability contours for the black hole masses measured for the other three confirmed and candidate events are also shown in light grey. (Adapted from Figure 2 of our publication).
We also estimated the distance of GW170104 and found that this event probably occurred about twice as far away as GW150914, at a distance of about 3 billion light years. In fact GW170104 is so remote that by the time its gravitational waves reached the Earth they had been stretched by about 20% due to the expansion of the Universe – a familiar phenomenon, known as the cosmological redshift, seen when observing the light from distant galaxies. A table showing all the best-fit parameters of GW170104 can be found in the published article, and can also be found in this fact sheet.
What does GW170104 tell us?
The population of stellar-mass black holes
GW170104 is the third, confirmed, direct detection of gravitational waves, and the fourth member (including the candidate event LVT151012) of our growing family ‘portrait’ of heavy black hole binary systems with directly measured masses. Figure 2 also shows how the estimated masses for the GW170104 black holes compare with those of the other three events; we see that GW170104 sits neatly in the gap between GW150914 and LVT151012. Moreover, its detection has improved our estimate of the global rate at which black hole mergers occur. Although this rate is still quite uncertain, it already appears to challenge some astrophysical models for how black holes might form and merge.
A further handle on these formation models can be obtained from measurements of black hole spin – since, for example, they make different predictions about how well aligned with each other the black holes’ axes of rotation should be. Although these spin parameters are not yet very well constrained, our observations do already hint towards a possible tendency for the spin axes in a merging binary system to be misaligned.
Testing General Relativity
The addition of a third, confirmed, gravitational-wave detection has also improved our ability to test some fundamental aspects of general relativity (GR). Combining our new observations with those of GW150914 and GW151226, we compared them with some specific GR predictions for the shape of the waveform, and searched for any systematic departures from those GR predictions in the data. The results were consistent with our previous findings (see here and here), meaning that Einstein’s theory once again passed the test with flying colors!
The large distance of GW170104 also allowed us to test another prediction of GR: that gravitational waves travel at the speed of light and, apart from the overall stretch due to expansion of the Universe, otherwise are not distorted. In some situations a wave can be dispersed as it travels through a material, meaning that the wave becomes distorted because components with different frequencies travel at different speeds. (Everyday examples of this phenomenon include the spreading out of white light into a rainbow. On the other hand, to a good approximation sound waves are not dispersed very much as they travel through the air in a concert hall, for example; if they were, then the audience at an orchestral concert would hear the notes from the piccolo and the double bass arrive out of step with each other). According to GR, however, the gravitational waves from GW170104 should not have been dispersed as they travelled across billions of light years to reach us. To test this we considered a simple model for the dispersion, motivated by some alternative theories to GR in which the phenomenon is predicted to occur, and compared these predictions with our GW170104 observations, again combining with our earlier observations of GW150914 and GW151226.
Figure 3 shows our constraints on the magnitude of the possible dispersion, for different values of another parameter, α, of the model. We see that only a tiny amount of dispersion is allowed in order to maintain consistency with our observations, meaning that the GR prediction (in which there would be exactly zero dispersion) again passed the test. Moreover, for the particular case of α = 0 our limits can also be re-cast to provide an upper limit on the mass of gravitons – quantum particles that make up gravitational waves in the same way that photons make up waves of light. Our new limit on the graviton mass, combining data from all three confirmed detections, improves by more than 50% on our previously published limits.
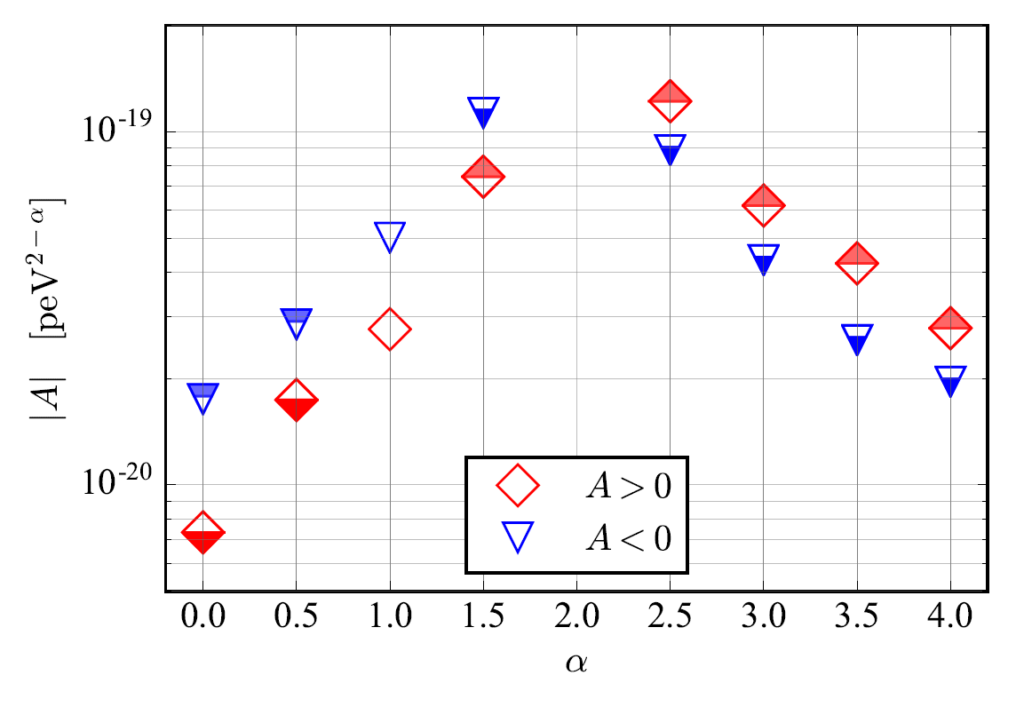
Figure 3. Upper limits on the magnitude of the dispersion parameter, A, permitted by the GW170104 data, for different assumed values of the other model parameter, α. The model allows for both positive and negative values of A, and we see that similar constraints are obtained in both cases. General Relativity predicts a value of A that is exactly zero.
The second Advanced LIGO observing run will continue until mid-2017, with Advanced Virgo also expected to begin data taking shortly. As more detections are added in the future, we can expect to gain further insight into models for the formation of stellar mass black holes, and to put General Relativity even more rigorously to the test.
Find out more:
- GW170104 detection paper, published in Physical Review Letters.
- LIGO Scientific Collaboration homepage
- Advanced Virgo homepage
- LIGO Open Science Center (with direct access to GW170104 data).

