Many of the stars in the nearby universe are not too different from our Sun: relatively small and long-lived, shining for billions of years. A small fraction, however, are much more massive, and burn their hydrogen “fuel” more rapidly. Over time these stars accumulate a dense core of heavier elements such as carbon and oxygen due to nuclear fusion. As the supply of hydrogen needed to fuel the fusion process becomes exhausted, the star’s core becomes increasingly dense and more and more pressure is needed to prevent it collapsing under its own gravity. Eventually the star is destroyed in a last, catastrophic burst of nuclear reactions—a supernova—and a portion of the star’s mass is expelled back into the surrounding interstellar space. However, a fraction of the star’s core cannot escape gravity’s relentless pull, and this matter collapses inward to form an immensely dense object, either a neutron star or, if the dying star is massive enough, a black hole—a region where gravity is so strong that nothing, not even light, can escape from it. Black holes formed in this manner could be up to tens of times more massive than the Sun. Neutron stars and black holes are much, much more compact than normal stars: They pack a comparable mass into a 100,000-times smaller radius. Therefore, black holes and neutron stars are collectively called “compact objects”.
A significant fraction of the stars that we see in our Galaxy are not alone; what we see as one point of light is, in many cases, actually two stars orbiting very close to each other. These are known as binary stars. If both stars in a binary were to form black holes it would produce a binary black hole system. These two black holes will eventually collide with each other due to emission of gravitational radiation. Directly observing for the first time the collision of two compact objects is the primary observational goal for gravitational-wave observatories, including Advanced LIGO and Advanced Virgo. The existence of black holes has been inferred from observations of X-ray binaries and from evidence predicting the existence of supermassive black holes at the center of galaxies, including our own. Gravitational wave observations will provide us with additional evidence for the existence of black holes, especially those in binary systems. As these objects emit no light or other electromagnetic radiation the only way to directly view black holes is through the gravitational radiation that they emit. Observations of black hole mergers will allow scientists to explore and better understand the complex nature of black holes: What is the distribution of black hole masses in the Universe? What is the distribution of the spin (rotational momentum) of black holes? Answering these questions will allow for a much better understanding of the mechanisms through which black holes are formed in the first place. Scientists could even begin to explore whether Einstein’s theory of general relativity accurately predicts gravity in the extreme environment of a black hole merger.
Advanced LIGO and Advanced Virgo are expected to begin observing the gravitational wave sky from 2015. They will detect the gravitational radiation emitted in three phases of a binary black hole collision; inspiral, merger and ringdown. The inspiral phase refers to the final few seconds before the objects merge, the merger phase refers to the actual collision of the two black holes. The ringdown phase is where the final black hole recovers from the titanic event from which it was formed. It is important that we can accurately understand how a binary black hole system will evolve through all three of these phases if we are to optimize our ability to observe them. To understand how this evolution will oocur, through all three phases, requires large-scale computer simulations. These precisely simulate the collision of two black holes to accurately predict their dynamics and therefore understand the gravitational waves that will be emitted during this process. These methods provide the waveform models that are needed, but are only accurate for the values of the black hole spins and ratio between the masses of the two black holes that were used to perform the numerical evolution. Thefore we require numerous simulations of a variety of black hole configurations to fully understand the systems that we want to observe.
The Numerical INJection Analysis (NINJA) project is a collaboration between scientists working on numerically modelling black hole collisions and scientists working to observe black holes in gravitational-wave observatories. The modelling community gains experience in how their simulations are used in gravitational-wave astronomy and obtains input into what black hole merger simulations should be performed in the future. The black hole astronomers gain a set of accurate waveforms that can be used to increase the sensitivity when searching for binary-black-hole mergers. The NINJA project has been running since 2007 and has already resulted in a number of important publications including results from an earlier phase of the project and tests of the waveforms used in this work. The project has been extremely worthwhile by enabling two communities of scientists to more easily work with each other to enhance the prospects of observing binary-black-hole mergers with gravitational-wave observatories.
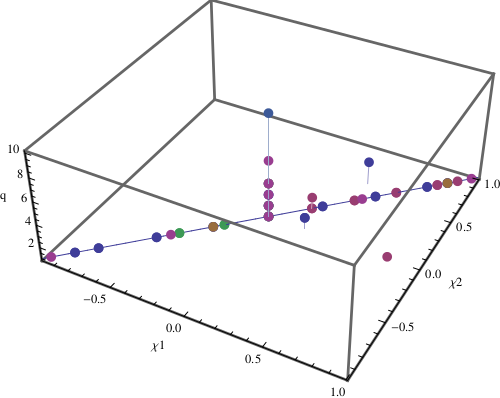
This plot shows the distribution of the mass ratio and spins of the waveforms that were submitted by numerical relativity groups for the NINJA-2 project. The 3 axes show the mass ratio between the two black holes “q”, and the spin of each black hole “χ1” and “χ2”. Each colored dot represents a waveform submitted by a numerical group for the NINJA-2 project, different colors represent different groups. As can be seen, the majority of waveforms that were submitted either had zero black-hole spins or were systems where both components had equal mass and equal spin.
Here we report on a new publication from the second NINJA project (NINJA-2). This work is the culmination of the second NINJA project and in it we investigate the ability to observe binary-black-hole mergers in 2015-16. For this analysis we created 7 simulated signals, which were added to data constructed from real Initial LIGO and Virgo detector data taken in 2009-2010, but modified to have a sensitivity equivalent to that expected from the early runs of the advanced detectors. The waveforms were created by stitching together the inspiral signal calculated from the known equations and the merger signal calculated from the numerical codes. The injection of the signals was at random times that were unknown to those analysing the signals. The data were searched using the same methods used in searches for real binary black hole signals. Six of the seven signals were determined to almost certainly be gravitational-wave signals, the remaining signal was placed at too great a distance to be recovered. We also perform the first investigations of how well we would be able to recover the masses and spins of the colliding black holes. Our tests demonstrate that, given the sensitivity predictions used in this work, Advanced LIGO and Advanced Virgo will be able to detect two merging black holes, about 1000-times farther away than the Andromeda galaxy if both black holes are 10-times as massive as our Sun. We also test whether Advanced LIGO and Advanced Virgo could determine from a gravitational-wave signal the properties of the objects emitting them: most importantly the masses of the colliding black holes. Indeed, this is possible albeit not with absolute precision or certainty (see the figure below for an example).
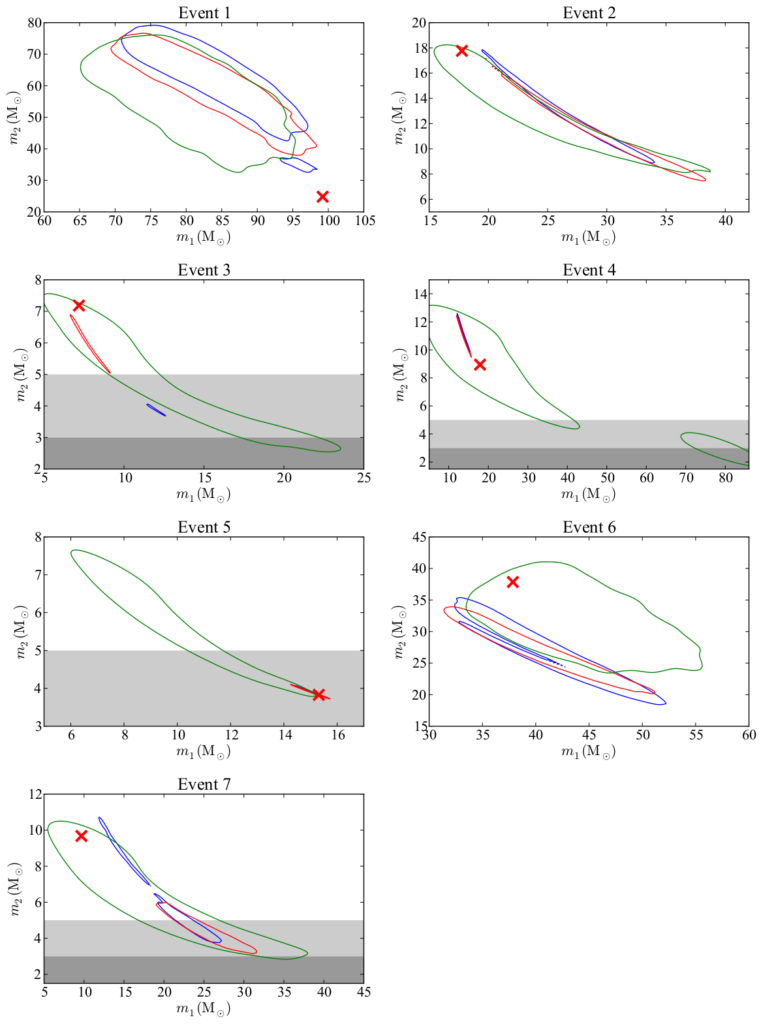
This plot shows how Advanced LIGO and Advanced Virgo would be able to constrain the masses of 7 simulated binary-black-hole mergers. Each colored curve denotes a 95% confidence region of the signal. This means that if we observe 100 signals that look the same as the example, then 95 of those signals would have actual masses contained within the region enclosed by the curve. We cannot measure the masses precisely because noise in the observatories can distort our measurements, so we can only constrain the masses to lie within a given region. The red and blue regions both correspond to estimates where we have assumed that the black holes have no spin. In some cases these give very poor estimates of the masses as only event 1 and event 5 had black holes with no component spin. The green region corresponds to an estimate where we do not assume the black holes to have no component spin, and therefore this gives more accurate, but larger, confidence regions. The light grey region corresponds to the so-called “mass gap”, where scientists have not yet observed any black holes or neutron stars with these masses. The dark grey region indicates the region where the lower mass black hole might be mistaken for a neutron star.
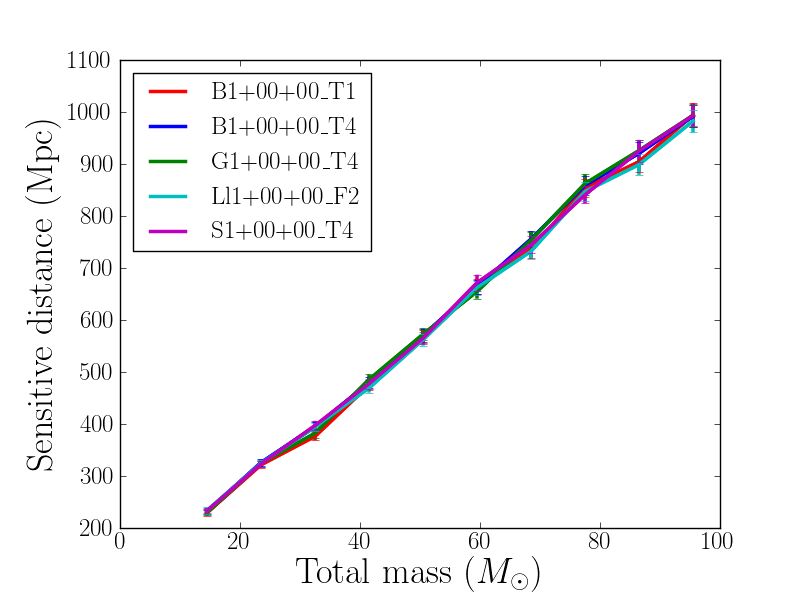
This plot shows the volume-weighted average sensitive distance to equal-mass non-spinning binary black hole mergers as a function of total mass for Advanced LIGO and Advanced Virgo in 2015-2016. The various colored lines show the sensitive distance for a variety of different numerical simulations of equal-mass non-spinning binary-black-hole mergers.

