The recent detection of gravitational waves from merging binary black hole systems (GW150914 and GW151226) has now opened up the exciting new field of gravitational wave astronomy. However, the signals from these black hole binaries were transient and were only observable in our LIGO detectors for the last second, or less, before they merged. The sources were also more than a billion light years’ distant, and so lay far beyond our own Milky Way Galaxy. The signals displayed a characteristic “chirping” form, in which the frequency, or pitch, and amplitude increased over the short duration of the signal. But, we are also searching for signals that could look quite different from that chirp pattern – for example sources that are constantly “on” (i.e. continuous) and emitting at an almost fixed (or monochromatic) frequency, like a pure audio tone.
An artist’s impression of a pulsar. Image credit: Joeri van Leeuwen, License: CC-BY-AS
One possible source of gravitational waves that could be much more local and would provide a continuous signal is a rapidly-rotating compact object known as a neutron star. We have known these objects exist ever since they were first observed as pulsars. They are the collapsed cores of massive stars that have run out of fuel and undergone a supernova explosion. With a mass of slightly more than the Sun’s (∼2.8×1030 kg) packed into a sphere of radius ∼10 km, neutron stars are about 40 trillion times denser than lead. A teaspoon of neutron star material would weigh about 10 million metric tons, roughly equivalent to the weight of a small mountain on Earth. Neutron stars are also spinning very rapidly, and for some their surfaces are rotating at up to ∼10% of the speed of light. So, these stars are very extreme objects! Our best understanding is that their pulsed emission comes from beams of radiation emanating from the magnetic poles of the stars acting like a lighthouse. If the magnetic and rotation axes of the neutron star are not aligned then a pulse is observed as the radiation beam sweeps across the Earth once per rotation.
To generate gravitational waves a pulsar must have some non-symmetric distortion in its shape – e.g. a “mountain” – that is not along its rotation axis. There are various ideas about how such a distorted star could form. The distortion could be “frozen” into the crust or core of the star after it was born in the supernova, or formed from material falling onto the star, or be produced and maintained through extremely large internal magnetic fields. However, due to the huge gravitational pull at the star’s surface, the material forming the “mountain” needs to be really strong so as not to be flattened out. A mountain on Earth made of jello, for example, could not get very big before collapsing under its own weight, but one made of solid rock can become as large as, or larger than, Everest. For a pulsar with a crust made up of “normal” neutron star material (highly distorted atomic nuclei, free electrons and neutrons) the maximum deformation that could be sustained before collapsing is about 10 cm, so not very high for a “mountain” (scaling up the relative dimensions this would be equivalent to a ∼50 m hill on Earth). If the star was made up from more exotic materials, e.g. if it were a solid quark star, then it could possibly sustain a “mountain” up to ∼10 m in height. The “mountain” size can also be expressed in terms of the star’s ellipticity (ε), which is a rough measure of the distortion’s size as a fraction of the star’s radius.
Making a few reasonable assumptions we can estimate the maximum amplitude of gravitational waves being emitted by most pulsars. To do this we use the law of conservation of energy. Pulsars are seen to slow down (known as spin-down) over time. This spin-down takes a very long time, and even the most rapidly spinning-down objects only decrease in frequency by less than a hundredth of a Hertz (or equivalently, increase their periods by less than ten microseconds) over a year. But, given the huge moment of inertia that the stars possess, this still represents a very large loss in rotational energy, corresponding to a power of ∼1031 Watts, or well over ten thousand times the Sun’s luminosity. If we assume that all of this energy is being lost by emission of gravitational waves we can calculate the amplitude with which we would observe those waves at the Earth. This is called the “spin-down limit“. When our searches are sensitive enough to reach below this limit we start probing interesting new territory, where gravitational wave signals could be detectable. We do, however, know that the spin-down limit is a naive upper limit, in that a large part of the spin-down can also be attributed to other mechanisms, such as magnetic dipole radiation.
Just as with the “lighthouse” model for their electromagnetic emission, gravitational wave signals are expected at a frequency related to the rotation rate, typically at twice this value. There are just over 430 known pulsars (see the Australia Telescope National Facility pulsar catalogue) spinning fast enough for their gravitational wave emission to be in the sensitive frequency band of the current Advanced LIGO detectors (∼20 to 2000 Hz). Our previous searches in LIGO and Virgo gravitational wave observatory data looked for gravitational wave signals from 195 pulsars, with the spin-down limit being surpassed for two of them (the Crab and Vela pulsars).
In this new analysis we have searched for a total of 200 of these pulsars using data from the first observing run of the Advanced LIGO detectors. To help reach the best sensitivity we have used information about these pulsars obtained through radio and gamma-ray observations; these have provided very precise knowledge of the pulsars’ positions, rotational frequencies, and how their frequencies change over time. This information has allowed us to accurately track any potential gravitational wave signal in our data over the whole length of the three-month science run (a search method called “coherent integration”).
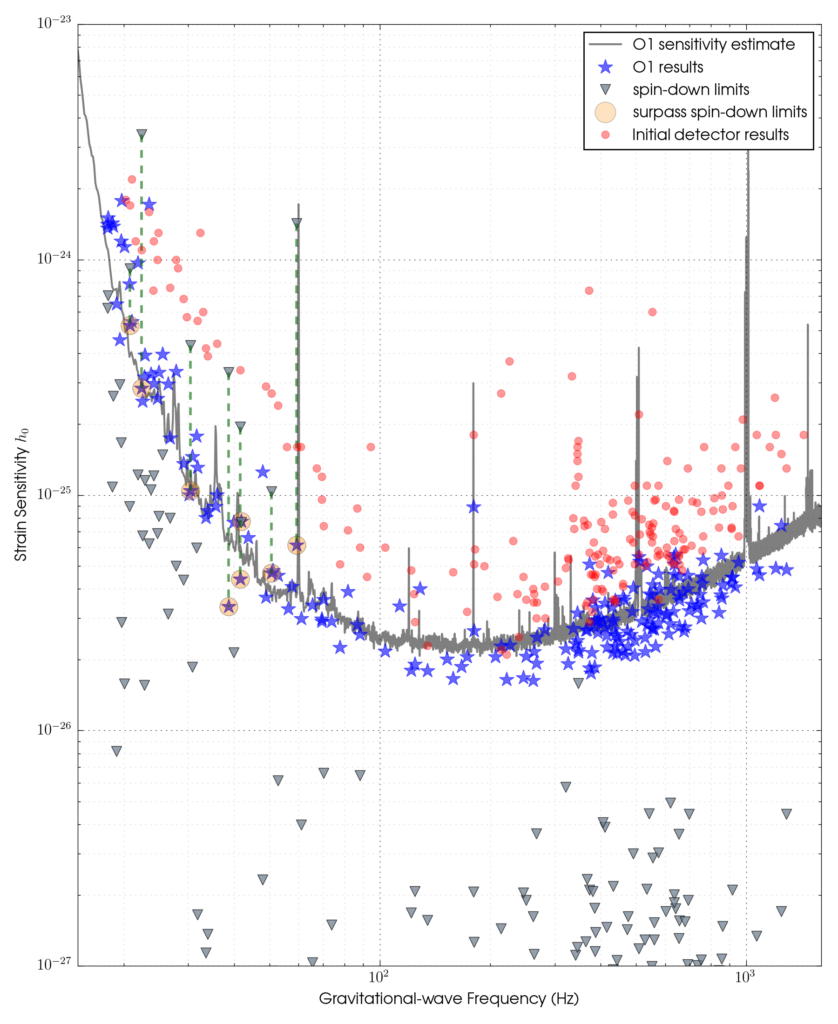
The stars in this plot show the upper limits on the gravitational wave strain amplitude for 200 pulsars using data from the first Advanced LIGO observing run. The triangles show the spin-down limits for a these stars. The pulsars for which our observations have surpassed the spin-down limits are highlighted with circles. The curve gives an estimate of the expected sensitivity of the run.
From these searches we were not able to detect evidence for gravitational radiation from any of the pulsars. But, we have produced the most sensitive upper limits yet, and for eight pulsars our observations have produced limits (using three largely independent statistical methods) on the gravitational wave amplitude that are below the spin-down limits. Two of the pulsars that have long been of interest for gravitational wave searches, due to their large spin-downs, are the Crab and Vela pulsars. These are the pulsars for which we have now surpassed the spin-down limit by a factor of 20 and 10 respectively. From this we can say that, respectively, less than ∼0.2% and 1% of their spin-down energy loss is due to gravitational radiation. We can also limit the ellipticity (roughly speaking the relative deformation, or “mountain” size, compared to the star’s total size) of the stars, and say that there are no “mountains” on the Crab pulsar greater than ∼10 cm in height, and none on Vela greater than ∼50 cm. Among the other pulsars, we found 32 more that are within a factor of ten of the spin-down limit. From the gravitational wave data alone we can limit the “mountain” size for some of these to less than ∼0.1 mm, although the spin-down limit is more stringent for those pulsars.
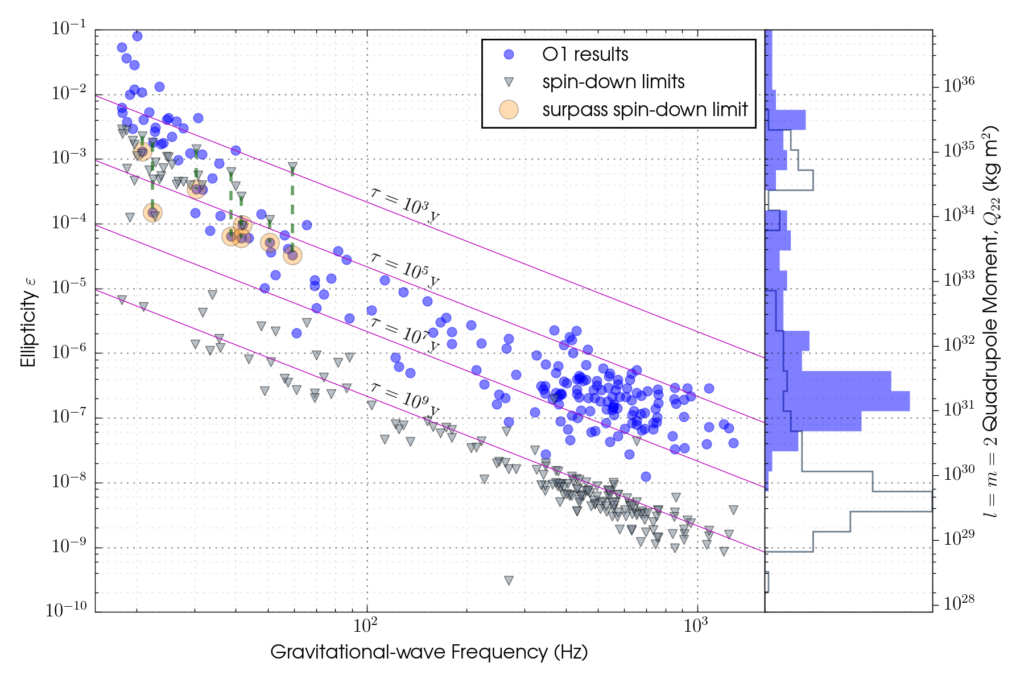
The filled circles show upper limits in terms of stars’ ellipticities ε, whilst the triangles give the equivalent spin-down limits. The ellipticity can roughly be converted to a “mountain” size using 25×(ε/10-4) cm (see Gravitational wave constraints on the shape of neutron stars for more detail). The diagonal lines show the ellipticities that would be required if a star had a particular characteristic age and was losing energy purely through gravitational radiation.
Future science runs of the Advanced LIGO and Advanced Virgo gravitational wave detectors will provide even greater sensitivity for known pulsar searches, and, at the very least, should allow us to surpass the spin-down limits for ten-or-more sources. Searches are also underway for continuous signals that are not associated with any currently known pulsars. These have to search the whole sky and a broad range of frequencies and spin-down values, making the searches computationally intensive, but opening up the possibility of observing previously unknown objects.
Read more:
- Freely readable preprint of the paper describing the details of the full analysis and results: “First search for gravitational waves from known pulsars with Advanced LIGO” by B. P. Abbott et al.
- A nice overview article on pulsars by Michael Kramer: Pulsars, EAS Publications Series, Volume 15, 2005, pp. 219-241 (freely available preprint of the overview)
- Chapter 6 of the book Essential Radio Astronomy by J. Condon & S. Ransom discusses pulsars and is freely available online.
- NASAs “Imagine the Universe!” page on pulsars

