Gravitational waves are a fascinating prediction of Albert Einstein’s theory of relativity. Unlike sound waves, which are air pressure variations, or light waves, which are electromagnetic oscillations, gravitational waves are “ripples” of the space-time itself propagating at the speed of light. Like music notes, the tones that compose gravitational waves carry information about their sources. The LIGO and Virgo observatories are chasing the “sounds” of catastrophic astrophysical events arriving from the nearby Universe. Some of them, such as a pair of neutron stars or black holes that inspiral and merge, produce a very distinctive “tune”, a waveform, that can specifically be searched for in gravitational wave data using “matched filtering” (like in another recent search). However, there are many other possible sources which may produce a broad range of different, sometimes uncertain, waveforms: these are targeted by searches for gravitational wave bursts.
The LIGO-Virgo network of gravitational-wave detectors comprises large laser interferometers located at distant sites (LIGO-Hanford in Washington, LIGO-Livingston in Louisiana and Virgo in Italy) which have collected data over the past several years, often simultaneously. Such a network allows for a multi-detector search with two main benefits: better ability to reject local noise (environmental and instrumental) in the individual detectors, and more uniform coverage of the sky. The detectors’ sensitivities have been similar enough that a gravitational wave signal should show up in all of the detectors at nearly the same time, with certain small differences depending on the arrival direction and polarization of the waves. Researchers in the LIGO Scientific Collaboration and the Virgo Collaboration have searched the data for any gravitational wave burst that might have arrived during that time, using a coherent search method that checks for consistent signals in all of the detectors simultaneously. The search algorithm used makes no assumption about the waveform, other than requiring that its signal power lies in the frequency range over which the LIGO and Virgo detectors were most sensitive, 64 to 5000 Hz. (See Figure 1.) This search technique has been developed and refined over the years, and most recently applied to data collected in 2009-2010 during the second joint run of LIGO and Virgo.
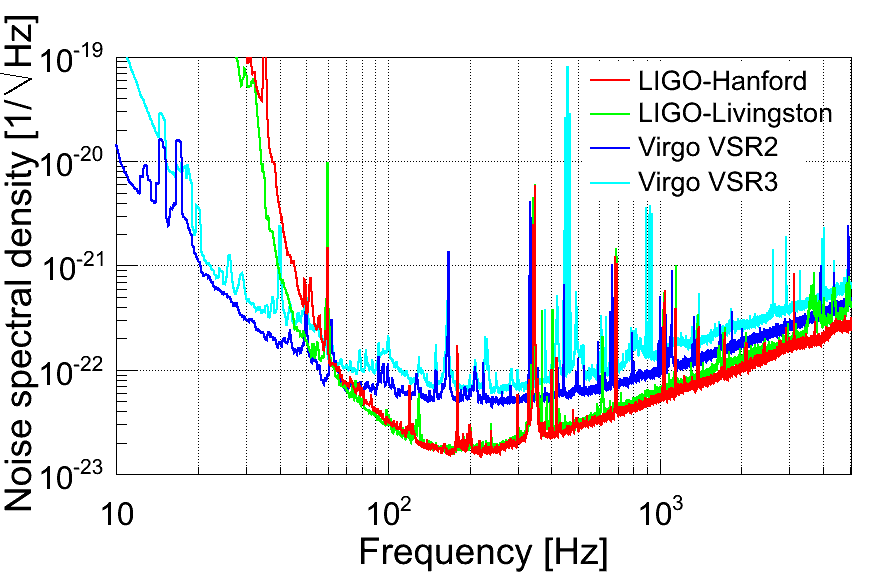
Figure 1. Sensitivities of the two LIGO detectors during their S6 science run, and the Virgo detector during its VSR2 and VSR3 science runs. Each curve shows the average detector noise as a function of frequency; a signal has to be significantly above the noise to be detected reliably. The vertical “spikes” are from mechanical vibrations in parts of the detector and multiples of the electric power line frequency, but are not too harmful since our analysis suppresses those frequencies and focuses on the lower-noise regions between the spikes.
Gravitational wave signals are expected to be extremely weak when they reach the Earth, so a crucial part of any search is to distinguish a real signal from the “background” of detector noise fluctuations. It is especially important for a burst search since there isn’t a certain expected waveform to compare to and any noise transient might be interpreted as a true gravitational wave signal. The background is sampled by first shifting the data from each detector in time, and then combining it. This allows to count the accidental coincidences due to noise fluctuations, while at the same time effectively scrambling any real gravitational wave signal that might be in it. By doing that many times with different time shifts, the background distribution as a function of noise strength can be determined rather precisely. A threshold is then set on the strength of candidate events in the data, which limits false alarms from background to a low rate.
No gravitational wave signal was detected in this search using 1.74 years of good quality data, including the previous LIGO-Virgo joint science run. Although disappointing, this “null result” is still quite informative, as it allows us to constrain models of gravitational waves emission and astrophysical source populations. Hence, the team turned to determining what signals could have been detected if they had arrived at Earth. In particular, the result constrains the rate for strong gravitational wave events (i.e. signals that would certainly have been detected) to be lower than 1.3 per year at 90% confidence level: we call this an upper limit. However, weaker events would not necessarily have been detected. The team mapped out the detection efficiency for gravitational-wave signals as a function of their waveform and strength by repeatedly adding simulated signals to the data and re-analyzing them. Figure 2 shows the resulting rate limits versus signal strength for several hypothetical waveforms.
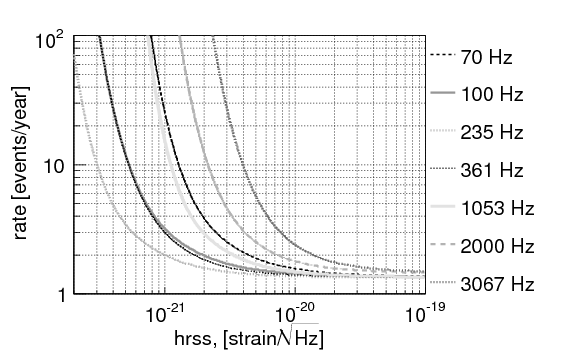
Figure 2. Upper limits on the rate of gravitational wave bursts, determined using the LIGO and Virgo data. The different curves represent signals with different characteristic frequencies; the vertical position of each curve shows what rate should have given us at least one detectable burst with 90% probability, for different assumptions about the strength of the burst (horizontal axis). Since no signal was detected, higher rates are ruled out with good confidence.
Figure 3 shows that our upper limit mainly depends on the detectors’ sensitivity at the characteristic frequency of the signal. In other words, at any given frequency, the data analysis algorithm was capable of detecting a wide range of simulated waveforms with comparable performance. So we can be confident that the search would have caught pretty much any type of gravitational wave burst that arrived during that time at the sensitivity level achieved by present detectors.
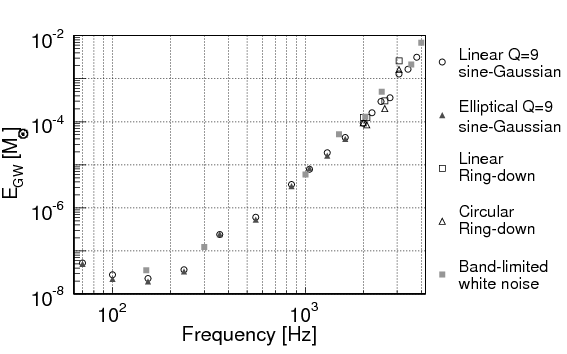
Figure 3. A study of the “generality” of the analysis, showing that it has rather similar ability to detect different types of signals as long as they have the same characteristic frequency (horizontal axis). Here, detectability is measured by the minimum amount of matter (as a fraction of the mass of the Sun) converted to gravitational wave energy that would produce a detectable signal, assuming that the source was 10 kiloparsecs (about 33 thousand light years) away, which is roughly half the Milky Way’s diameter.
Read more:
- Freely readable preprint of the paper describing the analysis and results: “All-sky search for gravitational-wave bursts in the second joint LIGO-Virgo run” by J. Abadie et al. (the LIGO Scientific Collaboration and the Virgo Collaboration)

