Many of the stars in the nearby universe are not too different from our Sun: relatively small and long-lived, shining for billions of years. But a small fraction are much more massive, and burn their hydrogen “fuel” more rapidly. These stars relatively quickly accumulate a dense core of heavier elements such as carbon and oxygen due to nuclear fusion. As the supply of fusion energy becomes exhausted the star’s core becomes increasingly dense and more and more pressure is needed to prevent it collapsing under its own gravity. Eventually the star is destroyed in a last, catastrophic burst of nuclear reactions — a supernova – and a portion of its mass is expelled back into the surrounding interstellar space.
But a fraction of the star’s core cannot escape the pull of gravity, and collapses inward to form an immensely dense object, either a neutron star or, if the dying star is massive enough, a black hole — a region where gravity is so strong that nothing, not even light, can escape from it. Black holes formed by stellar collapse could be up to tens of times more massive than the Sun.
In the work described in this summary, we are searching for gravitational waves from systems where two such black holes orbit round each other — a binary black hole — and finally merge into one. Gravitational waves are ripples in space and time, believed to be emitted when massive objects are accelerating or moving relative to one another. Due to their extremely high density, black holes should be some of the strongest sources of gravitational waves in the universe. As a black hole binary system emits gravitational waves, the black holes orbit faster and faster, gradually approaching each other. The animation below illustrates this in-spiralling motion, and shows how the pattern of gravitational waves reaching us from a distant binary black hole would evolve over time. This waveform is known as a chirp because of its rising frequency and increasing amplitude. We have converted the expected gravitational-wave signal to an audio track for the animation: it is a nice coincidence that the frequency of the waves corresponds to what we can hear!
Download movie (.MP4)
This animation illustrates the “inspiral” motion of a binary black hole system in the last few seconds before the two black holes merge into one, and the resulting gravitational-wave signal that might reach our detectors.
Top left: The signal waveform developing over time. Top right: A zoomed-in version of the top left panel showing the last few cycles of the waveform. At the end of the animation, the merger and ringdown phases can be seen.
Bottom left: A visualization of the orbiting binary system — black holes are represented by colored dots. The animation has been artificially slowed down by a factor of 4 to allow the details of the orbit to be seen. Bottom right: the binary orbit seen at an angle along the line of sight from the Earth.
At the end of the binary system’s evolution, the black holes get close enough to merge together into a single, larger black hole. This daughter black hole is at first distorted and asymmetric, but in a process known as a ringdown it emits a final burst of gravitational radiation and quickly settles into a quiet, symmetric state.
We searched for signals from merging binary black holes in data from the US LIGO detectors at Hanford (WA) and Livingston (LA) and the Virgo detector in Cascina, Italy. It is difficult to see gravitational-wave signals directly in the detector outputs because they inevitably contains noise caused by many other physical processes. We can carry out a more efficient search if we have accurate models of the gravitational waveforms that are likely to be emitted by binary black holes. To obtain such models, the equations of Einstein’s theory of general relativity describing the merger of two black holes must be solved numerically — one of the most technically challenging computations in physics, requiring weeks or months of supercomputer time.
The results of these numerical simulations are combined with theoretical knowledge of how the initial ‘chirp’ and final ‘ringdown’ parts of the waveform behave in general relativity, to generate families of complete waveforms. We use these to try and extract signals from the noisy detector outputs, and also to evaluate as accurately as possible how sensitive our search is. For instance, if there had been a merger of two black holes each 20 times as massive as the Sun, when the LIGO and Virgo detectors were operating at their best sensitivity, the signal could have been seen up to a maximum distance of about 300 Mpc (1 Mpc = 1 million parsec, about 3.2 million light-years) away from us — 400 times farther than the Andromeda galaxy.
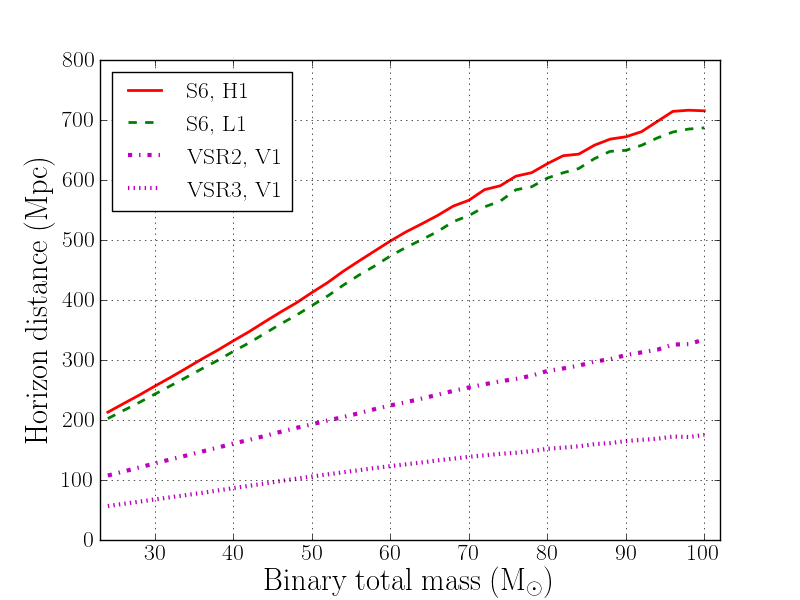
This plot shows the maximum possible distance (‘Horizon distance’) at which the merger of a binary black hole could be expected to produce a detectable signal, in each of the LIGO-Virgo detectors operating in their most recent science runs. We plot this distance for binary systems with equal black hole masses, up to a total mass 100 times that of the Sun.
If our search reveals a possible signal, we follow it up carefully by checking that the detectors were operating correctly at the time, and by a more detailed analysis of the data around the candidate. After all these checks were done, we did not find a convincing binary black hole signal in the most recent joint LIGO-Virgo data from 2009-2010. Since we did not observe a signal, we can set upper limits on the rate of binary black hole mergers happening in the local Universe — these limits are the most stringent to date. Knowledge of merger rates based on current astrophysical observations of black holes is extremely uncertain, so the limits resulting from our search can contain new information about how massive stars and black holes evolve.
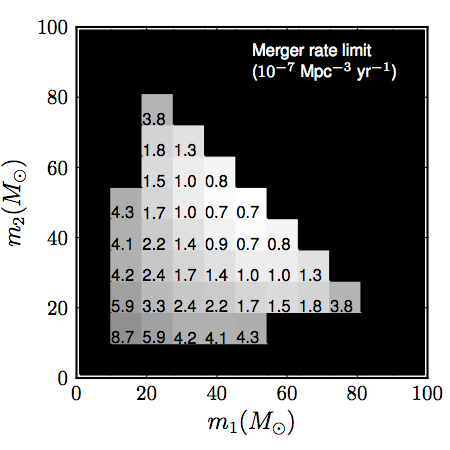
This plot shows the upper limits on massive binary black hole merger rates in the local Universe resulting from this search. We calculated the upper limit for possible binary systems of black holes with a wide range of different masses. The two black hole masses are shown on the axes (in units of the mass of the Sun) while the upper limit is given in units of mergers per 10 billion years per cubic Mpc (megaparsec) of space.
Beginning in 2015, an advanced generation of detectors (Advanced LIGO, Advanced Virgo, and KAGRA) will again be searching for binary black hole signals, but with significantly improved sensitivity and a much higher chance of finding signals. Some of the questions we hope to answer in future searches are:
- What happens when massive stars collapse: how much of their mass escapes, and how much falls into black holes?
- Are black holes in binaries spinning, and if so how fast?
- How do massive binary star systems evolve: is material transferred between the two stars, and how does the collapse of one affect the other?
- Do black hole binaries form mainly from binary systems of massive stars, or from random encounters between previously formed black holes?
- Does Einstein’s theory of general relativity give an accurate description of merging black holes?
The advent of advanced detectors makes us optimistic that we will soon make direct detections of gravitational waves. Such detections will not only help us not only to understand the behaviour of space-time under extreme conditions, but will also open a completely new window on the Universe, providing valuable information about the remarkable astrophysical objects that inhabit it.
Read more:
- Search for gravitational waves from binary black hole inspiral, merger, and ringdown in LIGO-Virgo data from 2009-2010, Phys. Rev. D 87, 022002 (2013)
- Preprint of the paper at arXiv.org.
- LIGO Document page with the paper and the data used in making the plots in the paper.
- Tutorial on gravitational wave science, including binary black hole collisions.
- Advanced LIGO
- Advanced Virgo
- KAGRA

