Neutron stars are remnants of the collapse of stars with masses in the range between about 8 and 20 solar masses. They are extremely dense objects, with a typical mass of about 1.5 solar masses and a radius of about 10 kilometers, reaching in the interior a density greater than that of atomic nuclei. Neutron stars can spin rapidly, the fastest known having a spin rate of 716 Hz. The details of neutron star structure are still largely unknown.
Isolated spinning neutron stars are among the targets of interferometric gravitational wave detectors such as Virgo in Italy, LIGO in the US and GEO600 in Germany. If these stars are not perfectly symmetric about their axis of rotation, e.g. if they have a “mountain” on their surface, they are expected to emit continuous gravitational waves. The motion of the gravitational wave detector around the Earth causes a frequency shift of the nearly sinusoidal received signal due to the Doppler effect, depending on the source position in the sky. Additionally, the emitted signal will slowly decrease in frequency as the star loses energy, not only in the form of gravitational radiation but possibly also as electromagnetic radiation, an effect called spin-down.
Among the roughly 1 billion neutron stars expected to exist in the Milky Way, only about 2500 have been observed through emission of electromagnetic radiation – mainly in the radio, gamma-ray and X-ray bands. We expect that there are a significant number of neutron stars that are not visible electromagnetically, either because the emission is too faint or because it is not directed at the Earth. These electromagnetically unseen neutron stars could also emit gravitational waves that would be observable by LIGO and Virgo. Moreover, we know from electromagnetic observations that there are several neutron stars with a high rotational energy loss. For many of them the rotational energy loss is high enough to be consistent with a detectable contribution from gravitational wave emission. In most cases these stars spin at a small rate. This makes the case for a low frequency search still more compelling.
We describe here the first search ever performed for continuous gravitational waves emitted by electromagnetically faint neutron stars spinning at low frequencies, below 25 Hz (corresponding to a gravitational wave frequency of 50 Hz). For this search we have used data from runs VSR2 and VSR4 of the Virgo detector, characterized by a very good low frequency sensitivity.
Gravitational wave searches for this kind of signals are complicated by not knowing the parameters of the source: position in the sky, gravitational wave frequency and the rate of spin-down. This means that a very large volume in the parameter space must be explored. The ideal data analysis strategy used to extract faint continuous wave signals from detector noise is “matched filtering”. This becomes computationally prohibitive when data stretches of the order of months or years are used and a wide fraction of the parameter space is searched over. To search for these signals using the available computing power, we use a ‘hierarchical’ approach in which the entire data set is broken into shorter segments, each roughly 2 hours in duration. Each segment is subject to a Fourier transform and the most significant peaks (local maxima above a certain threshold) in the time/frequency plane are selected. Each of these peaks is mapped to the frequency/spin-down plane of the source using the FrequencyHough transform.
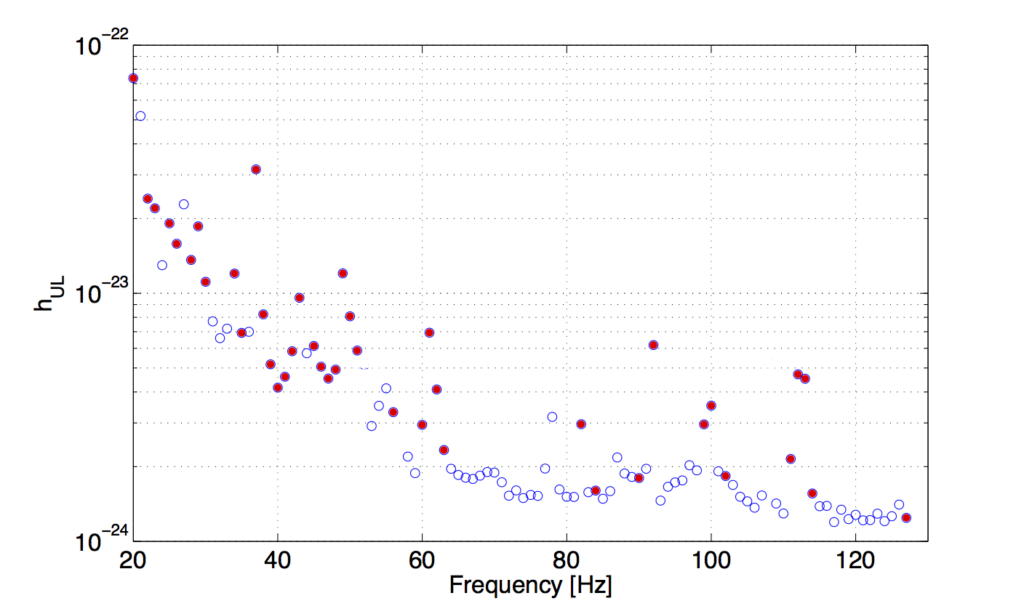
Figure 1. Upper limits on signal amplitude as a function of the frequency. We have computed one upper limit value for each 1 Hz band. Open circles refer to upper limits valid over the full corresponding 1 Hz band. Some 1 Hz bands, however, are very noisy and in such cases the upper limit has been computed excluding the most disturbed parts. Filled circles refer to these specific bands.
We have applied this method to an all-sky search for continuous gravitational wave signals over the frequency range between 20 Hz and 128 Hz and over a spin-down range between ~ -1.0 ⋅ 10-10 Hz/s to 1.5 ⋅ 10-11 Hz/s in the data of runs VSR2 and VSR4 of the Virgo detector. The results of our analysis do not show any evidence for the presence of a signal in the data, probably because there are no neutron stars emitting strongly enough in our frequency band to be detected at our sensitivity level. Therefore we can establish upper limits on the signal amplitude- i.e. limits on how large the signal could be, while still being consistent with our non-detection at a given confidence level. More precisely, the upper limit at, say, 90% confidence level is the amplitude value above which a signal would produce a result more significant than that we have obtained in the actual analysis 90% of the time. The upper limits we have obtained are shown in Figure 1. As an example, at the frequency of 80 Hz we can exclude the presence of a signal with amplitude of ~ 1.5 ⋅ 10-24 or higher with a 90% confidence level. The smaller the upper limit is, the more it constrains the population of galactic neutron stars. Our upper limits show an improvement of up to a factor of 2 with respect to the results of previous all-sky searches at frequencies below 80 Hz. In other words, we would have been able to detect signals, if present, up to two times smaller than previous searches. Figure 2 shows the so-called “astrophysical reach” of the search, that is the relation between the frequency, the spin-down and the distance for a potentially detectable source. Each set of points corresponds to a given distance value, while the dashed lines identifies the values of frequency and spin-down corresponding to a given ellipticity. For instance, considering a source at a distance of 100 parsecs and emitting a gravitational wave signal with a frequency of 80 Hz, it would have been detectable in our analysis if its spin-down was larger, in modulus, than about 2.8 ⋅ 10-12 Hz/s. This source would have an ellipticity larger than about 2 ⋅ 10-5. We do not know what are the typical ellipticities of neutron stars, but we expect that smaller values are more likely than larger ones.
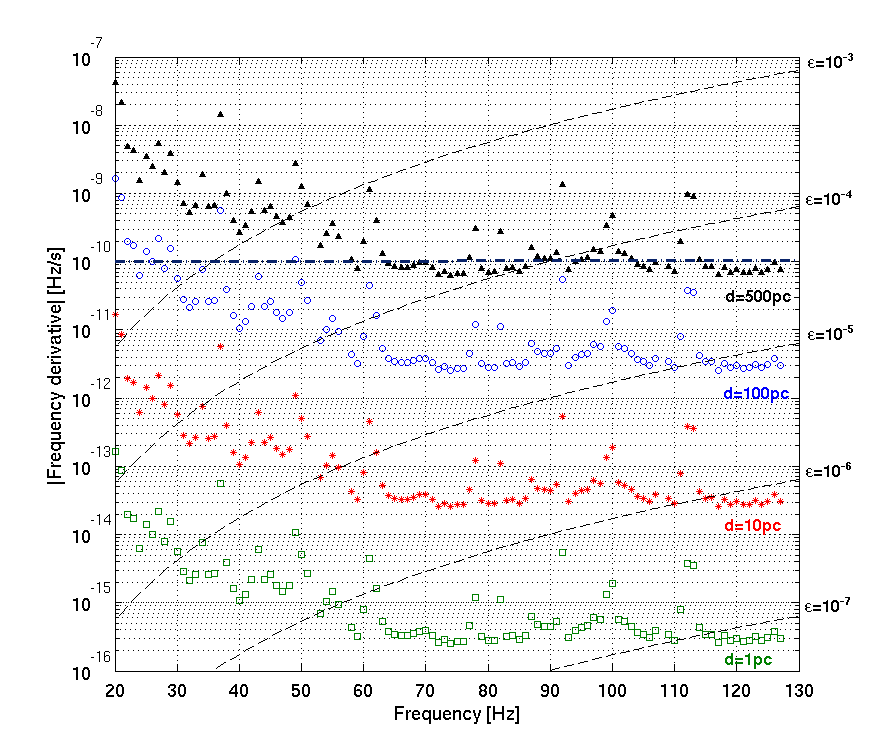
Figure 2. Astrophysical reach of the search. The sets of points give the relation between the frequency derivative (spin-down) and the frequency of a signal emitted by a detectable source placed at various distances. The triangles correspond to a distance of 500 parsecs; the circles to a distance of 100 parsecs; the stars to a distance of 10 parsecs and the squares to a distance of 1 parsec. The dashed lines represents lines of constant ellipticity. The horizontal dot-dashed line indicates the maximum spin-down value searched in the analysis.
Advanced LIGO and Advanced Virgo detectors will soon collect data with higher sensitivity. This will significantly increase the probability of observing continuous gravitational wave signals emitted by spinning neutron stars, even though a detection cannot be anticipated with certainty, given the lack of a precise knowledge of the neutron star structure, and especially the ellipticity. If successful, the detection of such kind of signals will provide a better understanding of many, still unknown, aspects of these fascinating compact stars.
Read more:
- Freely readable preprint of the paper describing the details of the full analysis and results: First low frequency all-sky search for continuous gravitational wave signals by J. Aasi et al.

