With GW150914, the first direct gravitational-wave detection, we got an unprecedented view of strong, rapidly changing gravity in action in our Universe. Here are some of the ways we used this observation to test our current best theory of gravity: Einstein’s theory of General Relativity.
General Relativity states that any accelerating masses will produce gravitational waves. But for us to be able to detect the waves the objects have to be extremely massive, and moving very quickly. For GW150914, the waves were produced by two black holes, orbiting each other at close to the speed of light, and finally crashing together to merge into a single black hole that shudders bit before settling down. Gravitational waves were emitted through all these stages. With decades of hard work, theoretical predictions for this entire process have been worked out in detail, following the fundamental rules of Einstein’s theory. We’ve used these predictions to translate the pattern of waves we received into an understanding of what produced them.
But we can also use what we saw to test General Relativity itself! We can compare different features of the observed signal with General Relativity’s predictions. And, while it may disappoint scientists who are always looking for unexplained observations and new challenges, the results so far show that General Relativity can explain everything we see. Here, we’ll go through a few of those tests.
Are there any unexplained features in the measured signal?
First, our parameter estimation for GW150914 has picked out the best choice of binary black hole signal from the array of possibilities that General Relativity allows: one produced by merging black holes with the particular masses and spins that we report in our detection paper. When we take out this best-fit signal, is there something in our data that’s left unexplained? No, all that’s left is a noisy data stream that we can’t distinguish from the type of noise we hear in our detector at other times. So all the gravitational-wave power that leapt out to us when we first saw GW150914 in our data is encoded in our General Relativistic model.
Is the signal self-consistent?
What other information do we have to work with? Figure 1 shows the range of gravitational wave possibilities, derived from General Relativity, that are compatible with the data taken by our instruments. As you’ve seen in the detection summary, the pattern comes from three phases of the binary black hole merger: inspiral, as the two initial black holes orbit and slowly fall toward each other as they emit gravitational waves, merger, as they crash together and become a single larger black hole, and ringdown, as the final black hole settles down to its resting state with a last few gravitational wave ripples.
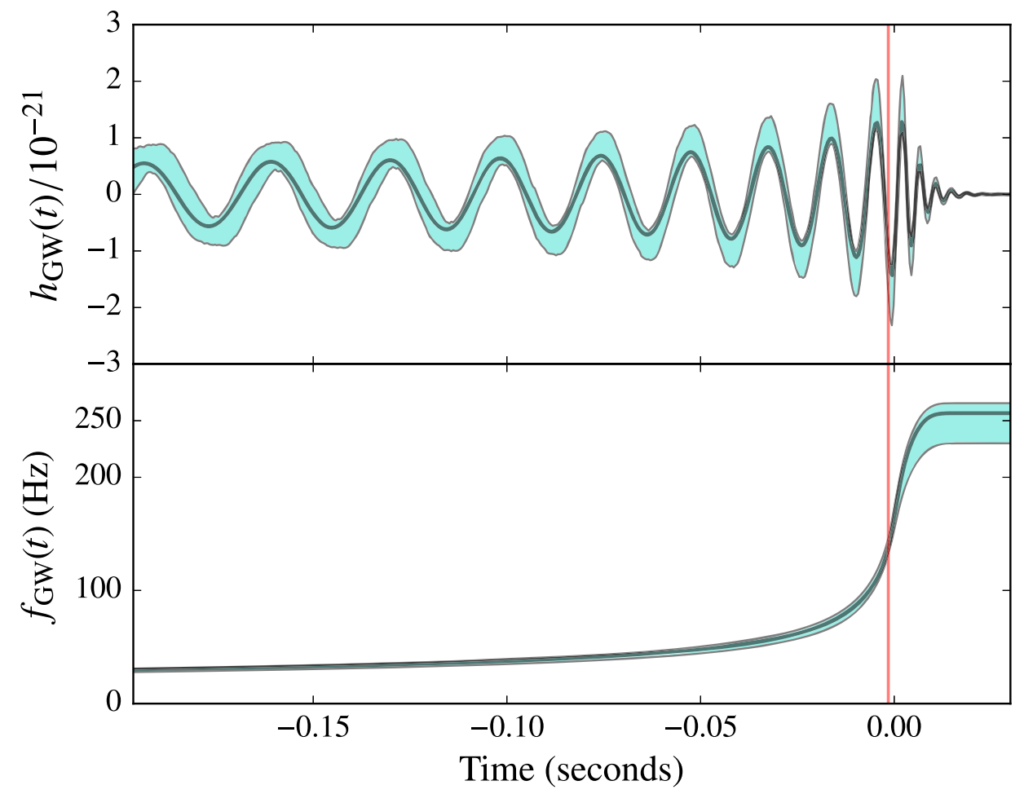
Figure 1 (Fig. 2 of our publication): Parameter estimation tells us that the gravitational wave pattern most likely lies within in the light blue band plotted above, with our best choice of waveform plotted in black. We divide the gravitational wave at the red vertical line: the inspiral is on the left, and the post-inspiral (i.e. merger and ringdown) on the right.
These phases are connected: if we know the mass and spin of the initial two black holes, the mass and spin of the final black hole are determined by our theory. That means we can check General Relativity by comparing the prediction based on the properties of the black holes before they merge – measured from the inspiral – with the characteristics of the final black hole that can be extracted from the post-inspiral, where the black holes collide and merge and the newly-formed black hole settles down. As it turns out, and as you can see in Figure 2, the results overlap. The properties deduced from the separate phases agree with each other in the way that General Relativity predicts.

Figure 2 (Adapted from Fig. 3 of our publication): The mass and spin of the final black hole can be determined from the observed gravitational wave in several ways. This image shows what range of values are allowed from different ways of studying the data, with a 90% likelihood that the values lie in the highlighted regions. The dashed line shows the prediction from the black hole masses that can be pulled out of the inspiral, while the dot-dashed line shows a post-inspiral result, using the high-frequency waves during merger and ringdown. The large overlap means the two are consistent. The thick black line shows the tighter constrains on the final black hole’s mass and spin that come from using the description predicted by General Relativity for all stages of the waveform together: Inspiral, Merger, and Ringdown, or IMR.
Details of how the black holes inspiral
We can also look closely at the details of the inspiral alone. Our description of the inspiral is constructed in a framework called “Post-Newtonian.” We start with Newtonian orbits (0PN), which are a good description when gravity is pretty weak and motion is slow compared to the speed of light. They work very well for our Solar System, allowing us to predict the positions of most of the planets and navigate spacecraft through interplanetary space. However, Mercury is close enough to the Sun that we need General Relativity to predict its orbit!
We can figure out how General Relativity would modify the motion, and the resulting gravitational wave pattern, when the modifications are small. This gives us our first Post-Newtonian “order” (1PN). We can then look at additional corrections if those modifications get a bit bigger (2PN), and then corrections to those, and keep on going until the calculations becomes too complicated. For technical reasons, there can also be “half-order” terms between these main steps. As we increase in PN order, we capture more of the full effect of General Relativity. The lower PN orders are important throughout the waveform, and the higher PN orders become more and more important as waves of higher frequency are emitted.
The result is a series of mathematical expressions, or terms, that describe, for example, how the frequency of gravitational waves emitted by a compact binary changes with time: one term for each Post-Newtonian order (including the half-values), and one numerical value to indicate how important that term is. We then compare this series with the way the GW150914’s frequency actually changed over time, shown in Figure 1, which generates a similar series of terms with a range of possible numerical coefficients that would describe the observed signal.
Comparing the two shows that the Post-Newtonian terms predicted by General Relativity work very well to describe our signal, and we can put unprecedented limits on how much individual numbers might depart from General Relativity’s prediction. The results are shown in Figure 3.

Figure 3 (Fig. 6 of our publication): This plot shows how the mathematical terms set by General Relativity compare with similar terms that describe the binary black holes that produced GW150914. The importance of each term is measured by a numerical value, or coefficient, and we are able to limit the differences between the real coefficients and those that General Relativity predicts. Before this observation, the best limits came from the binary pulsar system J0737-3039. Observations of binary pulsars tell us a lot about Newtonian orbits (0PN), but less about higher coefficients. Our new observation of gravitational waves puts the tightest bounds ever on the possible differences from General Relativity when gravitational interactions are strong.
We then do a similar analysis on parameters describing the merger and ringdown phases, and those parts of the signal are also consistent with General Relativity.
The speed of gravitational waves
Finally, we can also use our observation to check whether gravitational waves really travel at the speed of light. For the weak gravity of gravitational waves, we can describe the waves as a stream of gravitons—quantum particles that make up the gravitational wave the same way photons make up waves of light. In physics, only massless particles travel exactly at the speed of light, so a slower gravitational-wave speed means that the gravitons have some mass.
If the gravitons were to have mass, then it turns out that different massive gravitons will travel at slightly different speeds: slower if they are low-frequency gravitons, and faster if they are high-frequency gravitons. This means, for example, that the higher-frequency post-inspiral part of the signal would arrive a bit sooner than we’d expect from the low-frequency inspiral. However, we don’t see any evidence that this happens. Our results show that the graviton mass has to be about three times smaller than our previous largest-graviton-mass limit.
More tests to come
These are just a few of the tests that we have carried out using the LIGO data from GW150914, and General Relativity has passed every test we’ve thrown at it with flying colors. One hundred years after General Relativity, we have more and more evidence that Einstein was right! It’s amazing that these hundred-year-old ideas have held up to so much scrutiny!
But, of course, the story doesn’t end here. Advanced LIGO will continue to run, and we hope to catch more gravitational waves that we can use to repeat these types of tests. And, as Advanced LIGO improves in sensitivity, and as additional gravitational-wave detectors like Virgo and KAGRA come online, the signals should become louder and clearer compared to our background noise. So we’ll be able to raise even higher hurdles for General Relativity to leap – or not!

