The first direct detection of gravitational waves (GWs) in 2015 with GW150914 marked the dawn of a new era for astronomy. Since then, many more GW detections have been made, originating from different types of source. All of them have been compact binary coalescences, consisting of neutron stars (NSs) and/or black holes (BHs).
Here, we report the detection of GW230529, a compact binary coalescence observed on 29 May 2023, during the first part of the fourth observing run (O4a) of the LIGO-Virgo-KAGRA detectors, with one of the components of uncertain nature that has a mass larger than the expected range for NSs and smaller than the expected range for BHs.
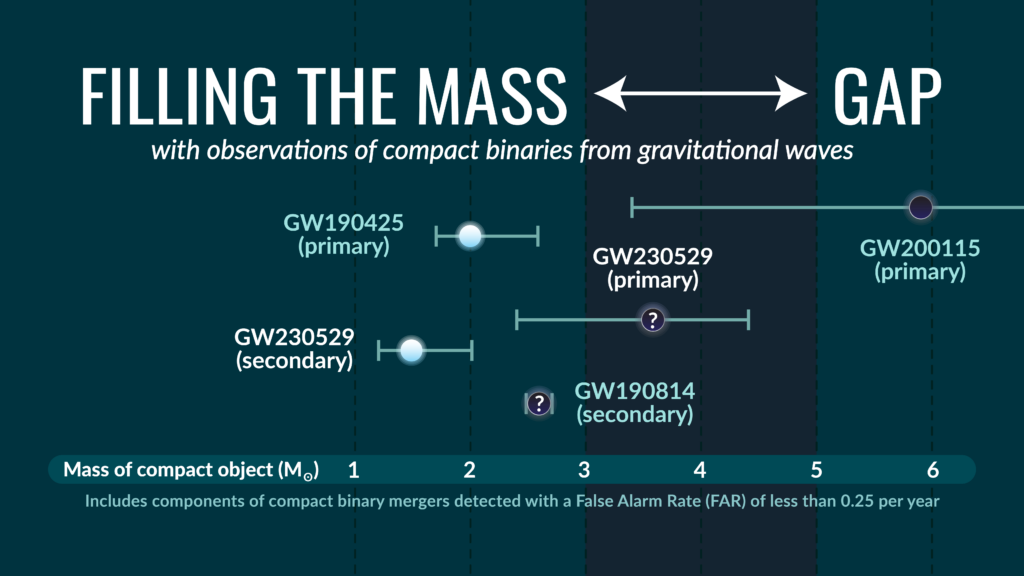
Figure 1: An illustration showing some of the component masses of gravitational wave events that lie within or around the 3 -5 solar mass region, also referred to as the “lower mass gap”. The light blue circles represent sources that are neutron stars, the black circles represent sources that are black holes, and the black circles with question marks indicate that the source is likely a black hole, but there is also a possibility it could be a neutron star. The primary mass of GW230529 is located in this mass gap. (Credit: S. Galaudage, Observatoire de la Côte d’Azur.)
How did we detect this event?
We analyze the data of each operating detector using the matched-filtering technique. This involves comparing detector data to predicted signals in order to find the prediction that matches best, in the case that a real signal is hidden in the data. This yields an estimate of the signal strength as a function of time, or, a signal-to-noise ratio time series. If there is indeed an astrophysical signal in the detector data the signal-to-noise ratio will be high, otherwise it will be low. This technique has proven to be efficient at identifying faint GW signals within the detector data, but it is not fool-proof. Various sources of noise can interfere with our measurements or even mimic GW signals.
How do we know that GW230529 is a real event?
Most of the time we search for signals that coincide both in time and source parameters in our different detectors. But we are not limited to searching for coincident events. We have refined our analysis techniques such that only a single detector is enough to confidently claim a detection, and fortunately so, because it allowed the detection of the exceptional GW230529 event, when the only usable data was from LIGO-Livingston. Three independent search pipelines (or search algorithms) reported the detection of GW230529. All of them use the matched-filtering technique but implement it differently and have developed powerful tools to discriminate astrophysical events from noise. The maturity of these search pipelines allows us to confidently cross-check their results. It is thus extremely unlikely that detector noise could have produced a signal such as GW230529. The event was detected during a real-time analysis of the detector data and the detection was verified at the end of the observing period. The event was reported with a false alarm rate of less than one per thousand years. This means that, in the absence of any compact binary coalescence signal in the detector data, we expect such a signal to occur in the noise by chance less than once every thousand years. We show in Figure 2 how this event stands out from the rest of the candidates.
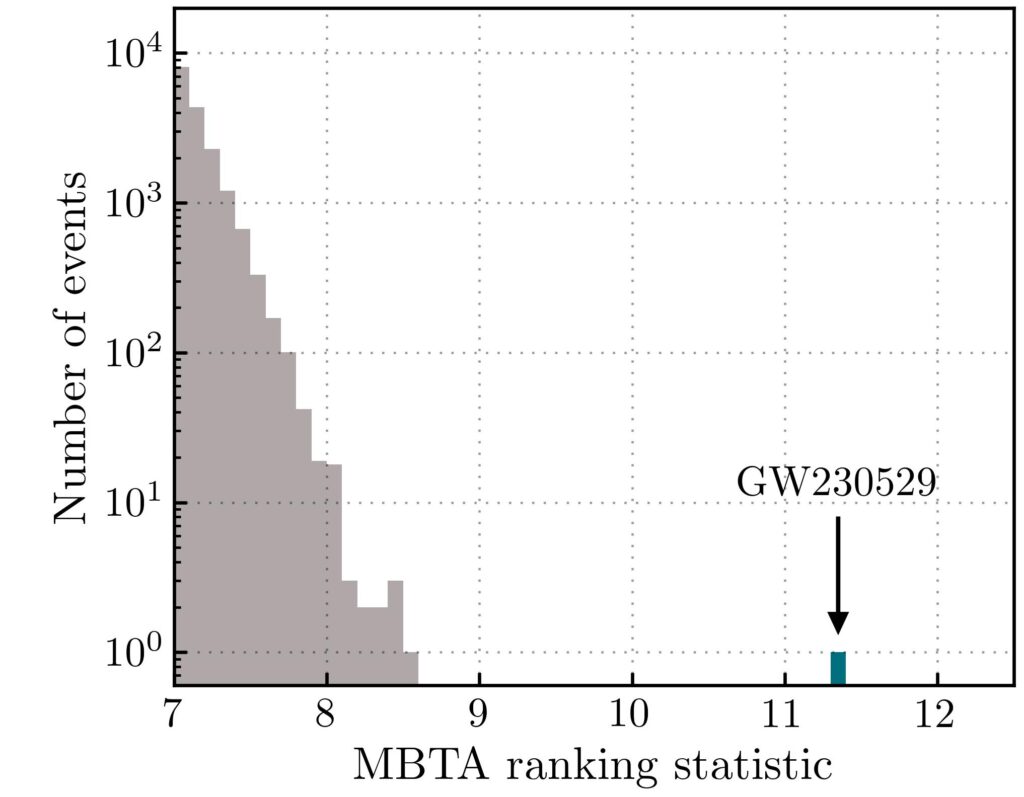
Figure 2: Ranking statistic distribution of one of the search pipelines (called MBTA) for all candidate events in LIGO Livingston during the first two weeks of the fourth observing run (O4a). The horizontal axis gives the value of the ranking statistic, which is used to rank search pipeline triggers and also incorporates various tests to discriminate against noise. The ranking statistic is derived from the signal-to-noise ratio; the larger the ranking statistic, the louder the event and the more consistent it is with an astrophysical signal. The grey distribution is for events that were not significant enough to be classified as being of astrophysical origin. The blue bin is for GW230529. We see that the ranking statistic for GW230529 is much larger than that of the rest of the events, with no events detected at a ranking statistic larger than about 8.5, other than GW230529 with a ranking statistic of 11.4.
Why is this event interesting ?
Scientists have proposed for several years the existence of a lower mass gap in the mass distribution of compact objects, between 3 M☉ and 5 M☉ (here M☉ stands for solar mass), where we expect few compact objects. However, recent observations of binaries through electromagnetic waves or GWs have proposed candidates for binaries with a component in the mass gap. For instance, the mass of the secondary object in GW190814 was estimated to lie, with very high probability, between 2.50 M☉ and 2.67 M☉ — higher than the heaviest neutron star known at the time of the detection but lower than projected BH masses.
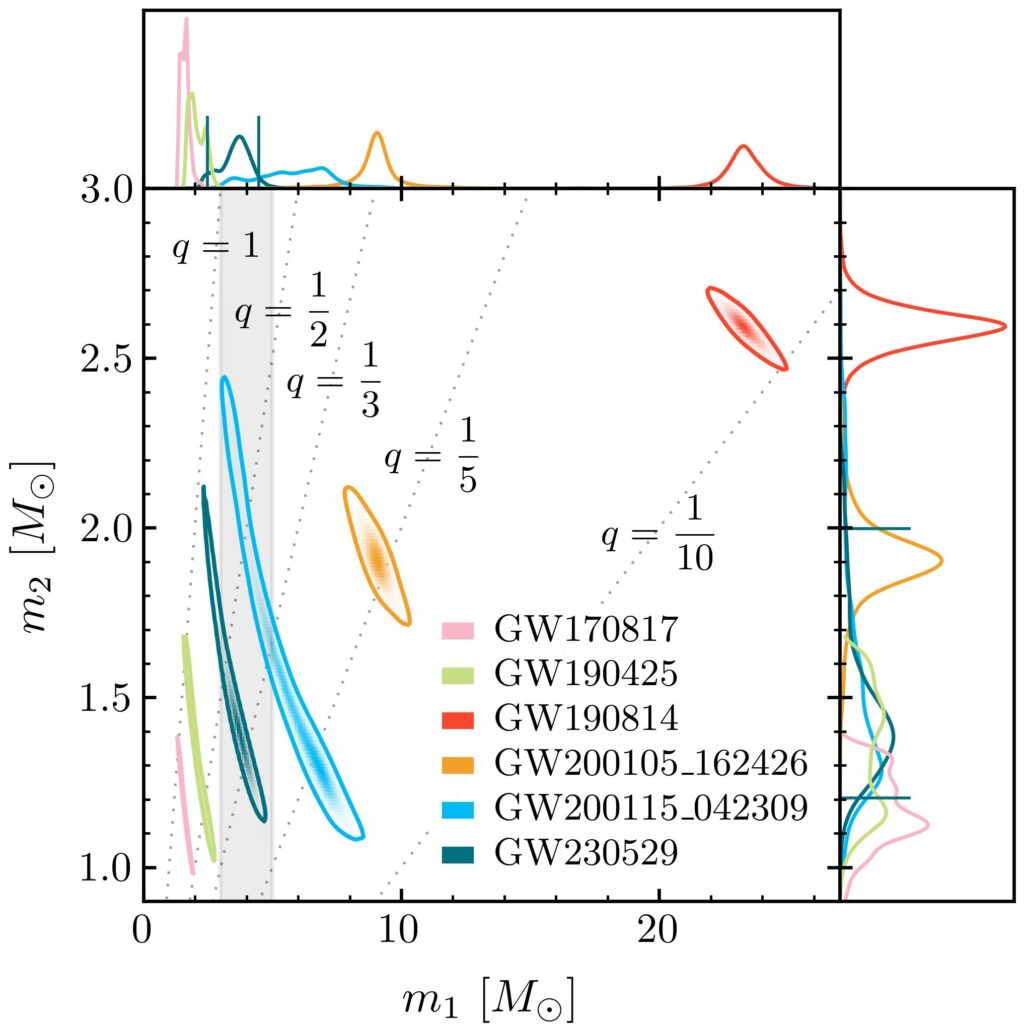
Figure 3: Probability distribution for the compnent masses of several binary systems. The most-likely values for the mass are indicated by the peaks in the probability distribution functions. The top plot is the projected distribution for the mass of the primary component and the right plot is the projected distribution for the mass of the secondary component. Dashed lines of equal mass ratio q=m2/m1 are also drawn. GW170817 (pink) and GW190425 (green) were consistent with BNS systems. GW200105_162426 and GW200115_042309 (orange and blue respectively) were consistent with NSBH systems. GW190814 (red) secondary mass may be either a black hole or a neutron star. The mass gap between 3 and 5 M☉ is shown as a shaded grey area. We see that GW230529 (teal) is right in between the two BNS and the two NSBH systems, with its primary mass in the mass-gap region.
With an estimated primary mass of about 3.6 M☉, GW230529 is the first binary candidate with the primary component in the mass gap, as shown by Figure 3. Given our current understanding of NS and BH populations, the primary mass is consistent (with a probability of 99%) with a BH of mass smaller than 5 M☉. However, the probability that the primary component is a NS was also estimated, taking into account our current knowledge from nuclear physics theory and experiment, as well as from astrophysical source populations. This probability of being a NS is small but non-zero, and under certain assumptions it can even reach a few percent; thus we cannot exclude this scenario with certainty. On the other hand, the secondary component of GW230529, the mass of which has a 90% chance of lying between 1.2 M☉ and 2.0 M☉, is almost certainly a NS.
What does it teach us?
NS-BH mergers are rare events. Therefore, every additional detection is extremely valuable for the study of merger rates — as well as to characterize the populations of BHs and NSs, which is one of the goals of GW astronomy. This means inferring the shape of their mass distributions, deriving the minimum and maximum mass for BHs and NSs and studying the abundance of rotating compact objects of different masses. Using only GW230529, the inferred merger rate for similar events is about 39 events per year in a volume of about 3.5×1028 cubic light-years. An analysis including other NSBH candidate events detected during the third observing run (O3) yields about 61 events per year in a volume of about 3.5×1028 cubic light years. Yet another analysis including additional, less significant, candidates gives a merger rate of about 95 events per year in a volume of about 3.5×1028 cubic light years. We find from these analyses that the inferred merger rate for binaries similar to GW230529 is comparable to the merger rate that was inferred during O3 for other events whose primary component was without doubt a BH. This reinforces the hypothesis that the primary component of the GW230529 binary system was a BH. The probability distribution for NSBH merger rates is shown in figure 4.
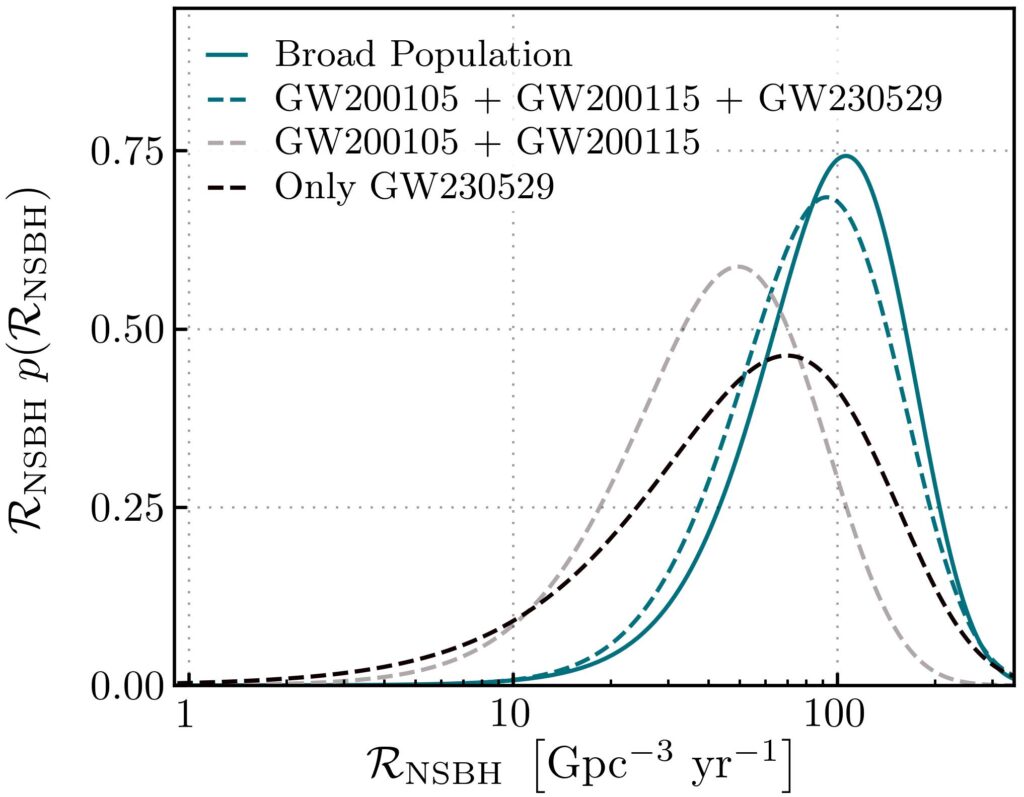
Figure 4: Probability distributions for the merger rate of NSBH systems. The probability distribution functions are peaked at the most likely value of the merger rate, shown on the horizontal axis. The dashed lines are derived using NSBH-only population models indicated in the caption. The solid line, denoted by “broad population” is derived using a population model that includes additional less significant events, as explained in the text. We see that the peak values for the various distributions are relatively close to each other in the sense that all populations overlap to some degree. In particular, the peak value found using GW230529 only is comparable to the peak value found when including other NSBH events.
Due to its primary mass being most likely in the mass gap, GW230529 is a prime candidate to refine population models. Three population models are considered, in order to study how they are affected by the observation of GW230529. The first two models encompass all types of compact-object binaries (BNS+BBH+NSBH) while the third one considers the NSBH population only. Including GW230529 in the first two models does not change significantly the outcome, meaning that GW230529 is not an outlier for these models. The third model, however, is significantly altered, as shown in figure 5. We see that in this case the abundance of low mass BHs is increased and the minimum mass of a BH is pushed towards lower values. When we include GW230529, we find a minimum mass of about 3.36 M☉ compared to the previous value of about 6.04 M☉ for this model.
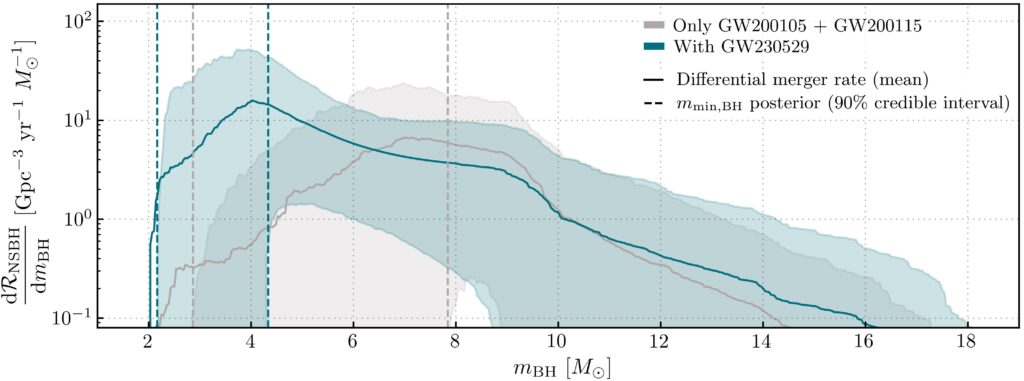
Figure 5: Merger rate of NSBH binaries (vertical axis) as a function of the mass of the BH (horizontal axis) in the system. The solid curves show the merger rates for two different models and the shaded areas show the uncertainties corresponding to these models. The dashed vertical lines show the expected range for the minimal mass of a BH, with 90% probability. The grey color considers an NSBH-only population model excluding GW230529. The blue color also includes GW230529 in the NSBH population model. We see that the inclusion of GW230529 increases the abundance of binaries with low mass black holes, as well as pushing the minimal mass for BHs towards lower values.
The formation process that led to GW230529 is uncertain. Current knowledge of core-collapse supernovae in massive stars disfavors such a scenario as the origin of the primary component in the binary due to its low mass. A more plausible scenario is a formation by fallback, where a BH forms after the supernova due to accretion of residual matter by the core. Recent results from numerical models showed evidence that formation of 3–6 M☉ black holes was possible through this formation mechanism. Simulations of core-collapse for helium stars have predicted BH masses as low as the maximum NS mass, although the mass range below 5 M☉ is less populated. To this day core-collapse models still carry large uncertainties regarding the outcome of the process, making it hard to determine with precision limits for the masses of compact objects. GW230529 is, therefore, a valuable asset for constraining these models.
Another possible scenario for the formation of the primary component is through a binary NS merger. In this case we can imagine that the secondary component is a member of a former triple or quadruple system, or that it was captured by the primary component while it was evolving in a young star cluster or an active galactic nucleus. We also cannot exclude a non-stellar origin such as a primordial black hole.
Further investigation of mass-gap systems like GW230529 will allow us to refine our understanding of BH and NS populations. This will in turn allow to better understand their formation mechanisms and, for NSs, their internal structure.
Find out more:
- Visit our websites:
- Read a free preprint of the full scientific article here.
Back to the overview of science summaries.

