A century ago, Einstein revolutionized our understanding of gravity with his general theory of relativity, which explains gravitational attraction as the curvature of spacetime around massive objects. It could be the case, however, that general relativity is only an approximation of a more complete theory of gravity, much like Newtonian gravity was an approximation of Einstein’s theory. To find out whether this is the case, physicists and astronomers put general relativity to the test, comparing the observed properties of gravity to the predictions made by this theory. Any disagreement between the two could signal that general relativity isn’t entirely correct.
The field of gravitational-wave astronomy, ushered in by Advanced LIGO’s direct detection of gravitational waves, gives us opportunities to test general relativity in many new ways. One new test is the study of gravitational-wave polarizations, which describe the characteristic pattern of the wave’s distortion of spacetime as it moves. General relativity makes specific predictions about the polarization of gravitational waves. In particular, Einstein’s theory only allows gravitational waves to take on two “tensor” polarizations. In contrast, alternative theories of gravity allow for up to four extra gravitational-wave polarizations (called “vector” and “scalar” polarizations). Whether a gravitational wave is tensor-, vector-, or scalar-polarized determines how it distorts spacetime and what direction it can move in as it propagates. (See Fig. 1 here for more details.) According to general relativity, vector and scalar polarizations do not exist. Any experimental observation of these “forbidden” polarizations would therefore prove Einstein wrong, indicating the existence of a complete theory of gravity that is more complicated that general relativity.
In this study, we have searched for any traces of the “forbidden” vector and scalar polarizations in the stochastic gravitational-wave background. Unlike the “loud” binary mergers detected by LIGO and Virgo so far, the stochastic background is a soft, persistent “hum” of gravitational waves produced by the combination of many quieter gravitational-wave sources. Although these quiet sources are too weak, too rare, or too distant to be detected individually, when they overlap they produce a long-duration background that appears as static noise in the Advanced LIGO and Virgo detectors. The strength of the stochastic background is typically described in terms of its energy density, which expresses the fraction of the total energy in the Universe in the form of gravitational waves. Advanced LIGO has previously searched for the stochastic background considering only the tensor-polarized gravitational waves allowed by general relativity. No such background has been detected yet; those searches instead yielded upper limits on the energy density (i.e. strength) of the background, over the whole sky and as a function of the sky direction. If a significant fraction of the stochastic background’s energy were instead in the form of the “forbidden” polarizations, then even a loud background could have been missed by previous searches.
In this latest analysis, we use data from Advanced LIGO’s first scientific observing run (which took place between September 2015 and January 2016) to answer two questions. First: Has Advanced LIGO found evidence of a stochastic gravitational-wave background of any polarization (“forbidden” or not)? Second: Is there any trace of the “forbidden” vector or scalar polarizations in the stochastic background? Ultimately, we find no evidence for a stochastic background of any polarization at the sensitivity of Advanced LIGO and Virgo during the first observing run, and by extension we cannot say whether the stochastic background contains vector or scalar polarizations.
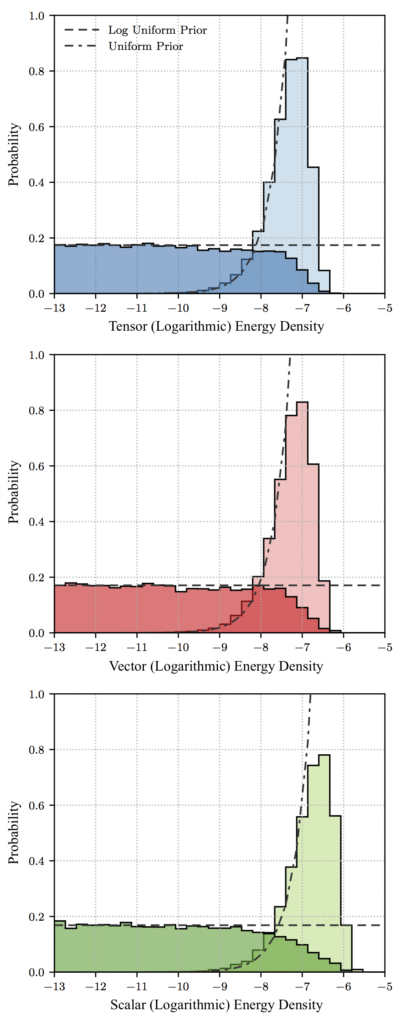
This figure shows the probability distributions for the energy densities of tensor- (top, blue), vector- (middle, red), and scalar-polarized (bottom, green) gravitational waves. Within each plot, the lighter and darker distributions show our results under two different priors (initial guesses) on the shape of the probability distribution of the strength of the stochastic background due to each polarization; these two priors are indicated by the dashed and dot-dashed lines. In the absence of a detected signal, our probability distributions match our priors at small energy densities (on the left-hand side of each plot) but sink to zero at large energy densities (right-hand sides). This behavior allows us to turn these probability distributions into upper limits on the possible strength of each polarization.
What we can do, however, is to place the first upper limits on the strength of vector- and scalar-polarized gravitational waves. The figure shows our inferred probability distributions on the energy densities of tensor- (blue), vector- (red), and scalar-polarized (green) gravitational waves in the stochastic background. The shaded shapes (or probability distributions) illustrate the possible energy densities that are compatible with our measurements — the higher a distribution at a given point, the more likely it is to represent the true value in our data. Notice that each plot in the figure contains two probability distributions. These just correspond to two different initial guesses (also known as “priors”) about the relative probability that the strength of the background might take for different values. Regardless of the prior used, we find that all probability distributions sink to zero above sufficiently large energy densities (towards the right side of each plot). We can therefore compute upper limits on the possible strengths of each type of polarization. 90% of the probability distribution of the strength of each polarization is contained within these limits, so the true value will be within the limit nine out of ten times. These upper limits imply that less than one millionth of the energy in the Universe comes from a gravitational-wave background of any polarization.
Trying to directly measure gravitational-wave polarizations is a powerful new test of general relativity. While we have not (yet!) detected a stochastic background of gravitational waves or found evidence for the existence of “forbidden” polarizations, this work presents the first upper limits on the energy density due to vector and scalar polarizations. Continued improvements to the sensitivity of Advanced LIGO and Virgo and the construction of additional detectors will allow for better resolution of the polarization content of gravitational waves in the future.
Read more:
- Freely readable preprint of the full publication describing the analysis and results
- Freely readable preprint describing the search for a tensor-only stochastic background
- Paper describing the detailed methodology of the search
- A search for “forbidden” polarizations using continuous-wave sources
- Advanced LIGO

