During the first and second observing runs (O1 and O2) of the Advanced LIGO and Advanced Virgo detectors, we have detected several gravitational-wave signals, ten from binary black hole mergers and one from a binary neutron star merger (click here and here to learn more). Binary mergers are not the only detectable sources of gravitational waves. Another important possibility is emission from asymmetric isolated neutron stars. If you already know what neutron stars and pulsars are you may want to skip to the analysis section.
This class of astrophysical object is produced after the death of a massive star in the catastrophic event known as a supernova explosion. Neutron stars are characterized by very strong magnetic fields and nuclear matter densities. Their mass can be between one to two times the mass of the Sun (about 2.0 x 1030 kg), but packed into a sphere of radius about 10 km, making the most massive neutron stars several dozen trillion times denser than lead. A teaspoon of neutron star material would have a mass of several billion metric tons, which is approximately equivalent to the weight of a large mountain.
Neutron stars spin around their axis of rotation, usually between 0.25 and 4 times every second. Some of them, such as the well known Crab pulsar, which are usually younger and brighter rotate between 20 and 60 times per second or even faster. There is also another class of pulsars, the millisecond pulsars, which can rotate even hundreds of times per second and are usually hosted in a binary system. To get an idea on how fast these stars spin, we can compare these numbers to the Sun’s rotational frequency, which is 1 rotation roughly every 24 days.
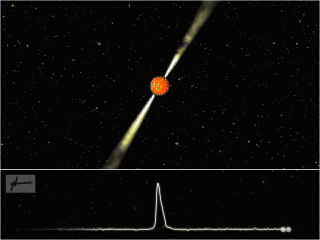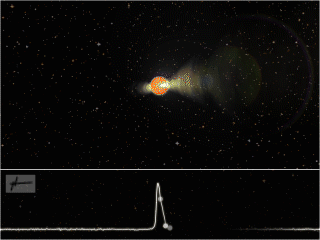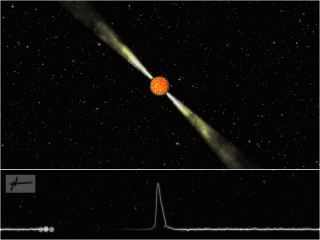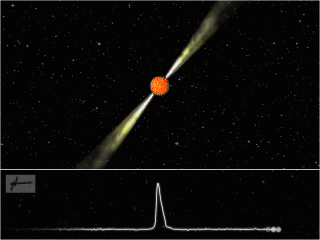
Artist’s impression of a pulsar. (Image credit: Joeri van Leeuwen. License: CC-BY-AS.) The lower panel shows the pulsed emission observed by our partner telescopes due to the beaming of the radiation, known as the “lighthouse effect.”
Many neutron stars can be observed using ground or space-based telescopes through their light emission in the radio, X-ray, and gamma-ray bands. Their emission strongly resembles that of a lighthouse (i.e., periodic pulses, as the light beam swings past an observer’s line of sight; see the upper figure). For this type of neutron star, referred to as a pulsar, the spin rate can be measured from the frequency of the observed pulses.
Einstein’s theory of general relativity predicts that gravitational waves (GWs) are emitted when massive asymmetric sources are accelerated. A symmetric object such as a perfect sphere emits no GWs, even if it is spinning rapidly. Neutron stars may be close to the most perfect spheres in the universe, but even they are not absolutely perfect spheres. Any departure from a perfectly symmetric spinning sphere will produce GWs. We use ellipticity as a quantitative measure of the departure of a neutron star from a perfect sphere. For example, if a neutron star has a small “mountain” on its surface crust, even as small as a centimeter above the average radius of 10 km, that will result in an ellipticity of around 10-6, and GWs will be emitted.
It has been observed that pulsars are slowly spinning down (typically by 1 rotation per second every 1000 years or longer!). Theoretically, a fraction of their rotational energy loss can be explained through the emission of GWs. The maximum amplitude of GWs that can be emitted due to energy conservation is referred as the spin-down limit. Consequently, the detection of GWs emitted by neutron stars will help us to answer the question “How much energy does the star lose via gravitational waves?” This, in turn, will help us understand how much a typical neutron star deviates from spherical symmetry.
Unfortunately, GWs from neutron stars are expected to be very weak; it seems that, given the detectors sensitivity during O2, these signals did not have enough signal-to-noise ratio to be observed yet.
Analysis
The optimal method to disentangle a GW signal from detector noise is called matched filtering. In this method, we compare the data to theoretical or simulated templates which predict the expected gravitational waveforms. For rotating neutron stars, the templates are described by two key physical properties, or parameters, of the star: the star’s rotation speed (frequency) and its spin-down rate. Specifically, the templates are essentially sinusoidal waveforms with frequency equal to twice the frequency of the light pulses, but with this frequency changing slightly over time due to the spin-down and the detector motion with respect to the star. In principle, we can search for a specific pulsar by using a template with frequency and spin-down rate matching those we find by observing the pulsar with our partner telescope facilities. However, even a small mismatch in these two parameters would be enough to prevent a detection of GWs. There are reasons to believe that there may indeed be small mismatches; for example, the actual frequency may differ from the predicted value due to the nature of the matter in the rapidly rotating star, or due to imperfect measurements of the light pulses. To account for this, we make use of GW templates with frequencies in a narrow band around the frequency derived from the light pulses. We refer to these as “narrow-band searches”.
In our previous narrow-band search we have targeted 11 known pulsars for which we expected to constrain the GW energy emission. With the improved sensitivity and longer observation period of O2, we have extended our target list to include all radio pulsars for which we expected to surpass the spin-down limit, or at least come within a factor of 10 from it, based on the expected sensitivity of the new narrow-band search. This choice was due to the fact that pulsar distances (which are needed to compute the expected GW amplitudes) can have large measurement errors. The new targets include low-frequency radio pulsars such as J0940-5428 and J1747-2809 and also a few millisecond pulsars (which are pulsars with a rotational frequency higher than 100 Hz) such as J1300+1240 and J2124-3358. Unfortunately, we find no evidence for the presence of a GW signal from these pulsars. This result is not surprising for the pulsars that have spin-down limits below the detector sensitivity (assuming the pulsar distances were correct). On the other hand, for other pulsars, we have been able to put constraints on the GW energy emssion which are below the spin-down limit. In this cases, we have successfully set an upper limit on the GW energy emission.
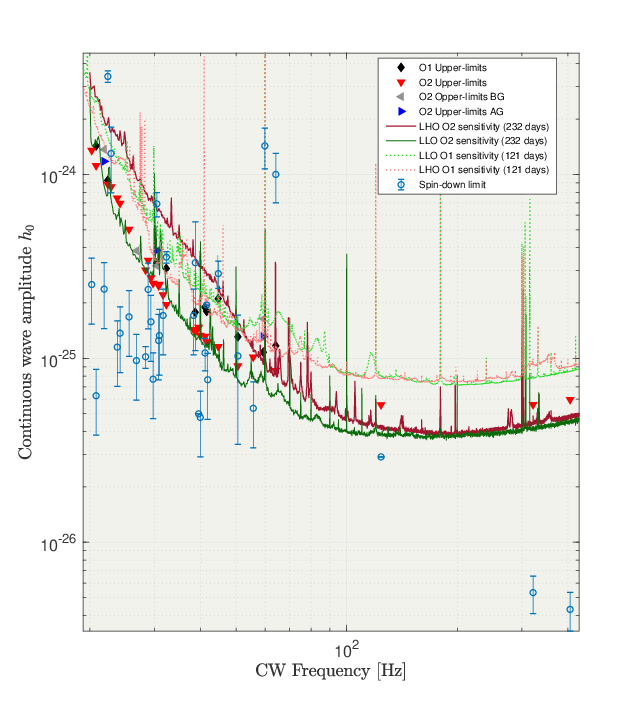
Vertical axis: CW amplitude, horizontal axis: searched GW frequencies. The different lines indicate the estimated search sensitivity for O1 and O2 narrow-band searches, while the different markers indicates ULs that we have found in these searches. The error bars correspond to the uncertainties on the pulsar distance and correspond to 68.3% confidence level.
We can evaluate upper limits to the GW amplitude, and, assuming a distance value, also the corresponding star’s ellipticity. If the upper-limit is below the spin-down limit, it means that we are constraining the GW emission with our search. In other terms, if a neutron star would have emitted a GW stronger than our upper-limit, then we would have detected it in 95% of the cases. With the O1 narrow-band search we already constrained the GW emission in a narrow-frequency band for several pulsars, however with the O2 search we are drastically increasing the number of pulsars for which we have set limits on the GWs emission. In fact, we have been able to constrain the GW emission from some of the pulsars for which we didn not surpass the spin-down limit in O1, such as J1400-6325, J1813-1246, J1833-1034 (the second most energetic pulsar after Crab) and J1952+3252. Moreover, we have constrained the GW emission for new targets considered in this search such as J0940-5428 and J1747-2809. Most importantly, with this narrow-band search we constrained the GW energy for the first time for the pulsars J1400-6325, J1833-1034 and J1747-2809.
Read more:
- Full text of the O2 narrow-band search described in this article, “Narrow-band search for gravitational waves from known pulsars using the second LIGO observing run” by B. P. Abbott, et al. (LIGO and Virgo collaborations): Free preprint or peer-reviewed journal article.
- Full text of the O1 narrow-band search, “First narrow-band search for continuous gravitational waves from known pulsars in advanced detector data,” by B. P. Abbott, et al. (LIGO and Virgo collaborations): Free preprint or peer-reviewed journal article.
- Paper describing the method employed for narrow-band searches, “Method for narrow-band search of continuous gravitational wave signals,” by P. Astone et al.: Free preprint or peer-reviewed journal article.
- Paper describing the implementation of the narrow-band algorithm, “An improved algorithm for narrow-band searches of continuous gravitational waves,” by S. Mastrogiovanni et al.: Free preprint or peer-reviewed journal article.

