Tests of general relativity with gravitational waves from black hole mergers

Einstein’s theory of General Relativity has passed a large number of tests in the over 100 years since its conception. The observation of gravitational waves emitted by two coalescing black holes was one of the most anticipated discoveries in the history of General Relativity, and Einstein was proven right again. With the emerging field of gravitational-wave astronomy, we can use the gravitational-wave signals from merging black holes to test Einstein’s theory in the strong field regime for the first time ever, an environment not achievable in any laboratory.

Novel tests of General Relativity with gravitational waves have been performed on the binary neutron star merger GW170817, and on previous black hole mergers, such as GW150914, GW170104 and GW170814. Here, we perform these tests on all the confidently detected binary black hole merger signals reported in the Gravitational-Wave Transient Catalog 1 (GWTC-1). We also combine together the results of the analyses on the most confident detections to obtain our strongest constraints on deviations from the predictions of General Relativity to date. However, we are not able to perform all the tests on every signal. Some tests require either the low- or high-frequency parts of the signal to be sufficiently loud, and the relative loudness of these parts of the signal is different for different binaries. This difference primarily depends on the binary’s total mass, which determines which parts of its signal lie in the frequency regions where the noise in the detectors is lower.

Comparing the data with our waveform estimate

When we find a gravitational-wave signal, we use analysis techniques to measure the properties of the source, as explained here. With these measurements, we can then compare the data with the model gravitational waveform that best matches the observed signal. This model waveform is constructed using the predictions of General Relativity. Hence, if the model cannot explain all the power present in the signal, we would have to reconsider if the theory we are using is correct, or if we are missing some important physics not accounted for in the construction of the model. We have found no evidence for extra power in our black hole binary signals, and the result of subtracting the best-matching model waveform from the data is consistent with the detector noise present at any other time.

Testing the agreement between different parts of the signal

There are three stages in the coalescence of two black holes: the long inspiral phase, where the two black holes are orbiting each other; the merger phase, where the two black holes collide to finally become one larger black hole; and the ringdown phase, where the remnant black hole emits gravitational waves while settling down to its final resting state. General Relativity tells us what the mass and spin of this final black hole should be, based on the masses and spins of the initial inspiraling black holes. We can thus test the theory by checking if we obtain the same final black hole properties from the measurements in the inspiral stage of the signal and from the measurements in the merger-ringdown stages. The contours in Figure 1 represent the 90% probabilities that the difference between the two separate measurements lies within the area of the contour, known as the 90% credible region. All individual event probabilities, as well as the total resulting probability when combining all events, are compatible with the prediction of General Relativity, represented by a black cross in Figure 1.

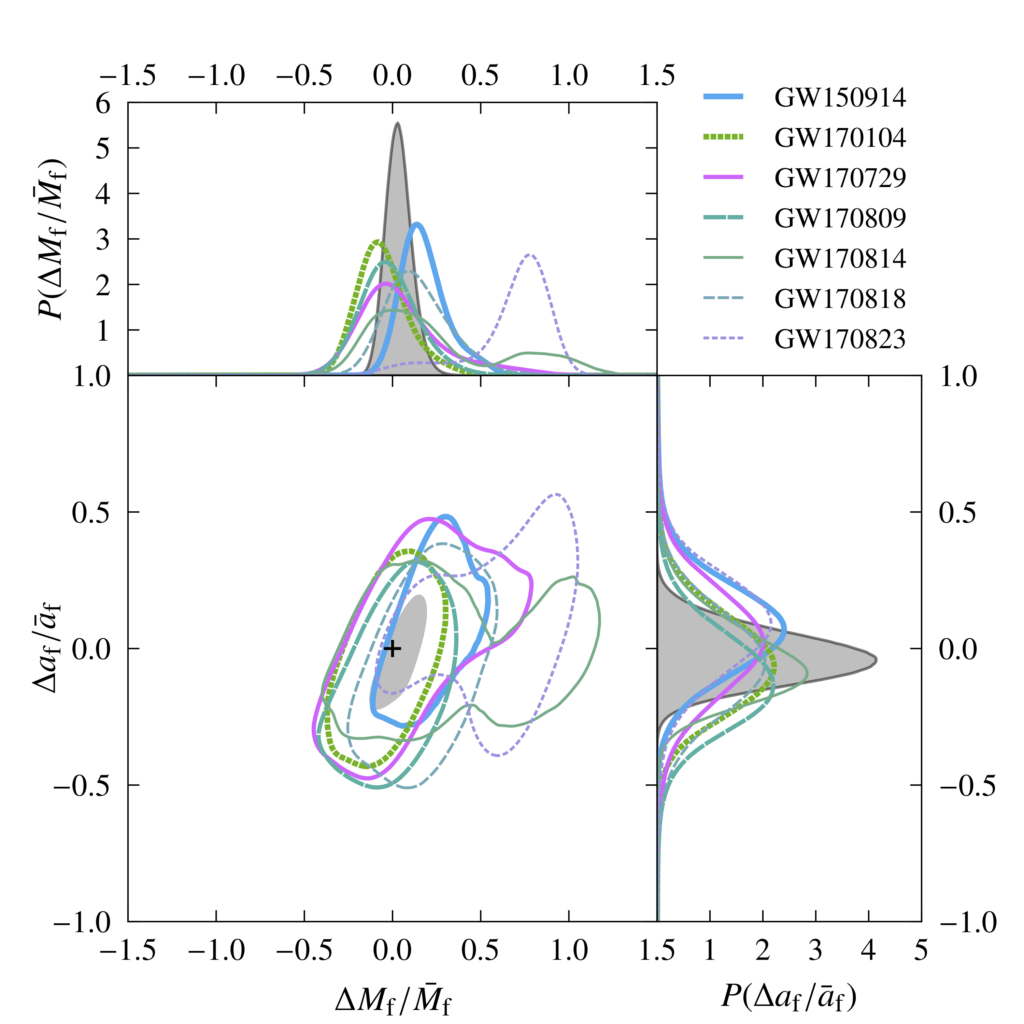
Figure 1: 90% credible region for each event of the difference in the final black hole’s mass, Mf, and spin, af, as measured separately from the inspiral and the post-inspiral parts of the signal (Figure 2 of our paper). The grey shaded region is the result of combining events together. The black cross at zero indicates exact agreement between the two measurements, as expected if General Relativity is correct.

Possible deviations in the gravitational waveform from General Relativity

General Relativity describes how two black holes orbiting each other generate gravitational waves, losing energy in the process and getting closer together until they merge. We use these predictions of General Relativity to construct gravitational waveform models. While there are not yet any waveform models for binary black hole coalescences in other theories of gravity to compare with (they are very difficult to calculate!), we can still test the predictions of General Relativity by introducing small modifications to our currently available waveform models and compare the data with these “distorted” waveforms. We saw here that the inspiral stage of a binary merger is well described by a series of terms arising from the post-Newtonian (PN) formalism, which add corrections to Newtonian gravity to include the most important effects of General Relativity. Introducing deviations in these PN terms, we test the inspiral part of our waveforms and obtain good agreement with General Relativity for all the binary black holes we have analyzed. In Figure 2 we give the upper limits on the magnitude of the deviations from General Relativity.

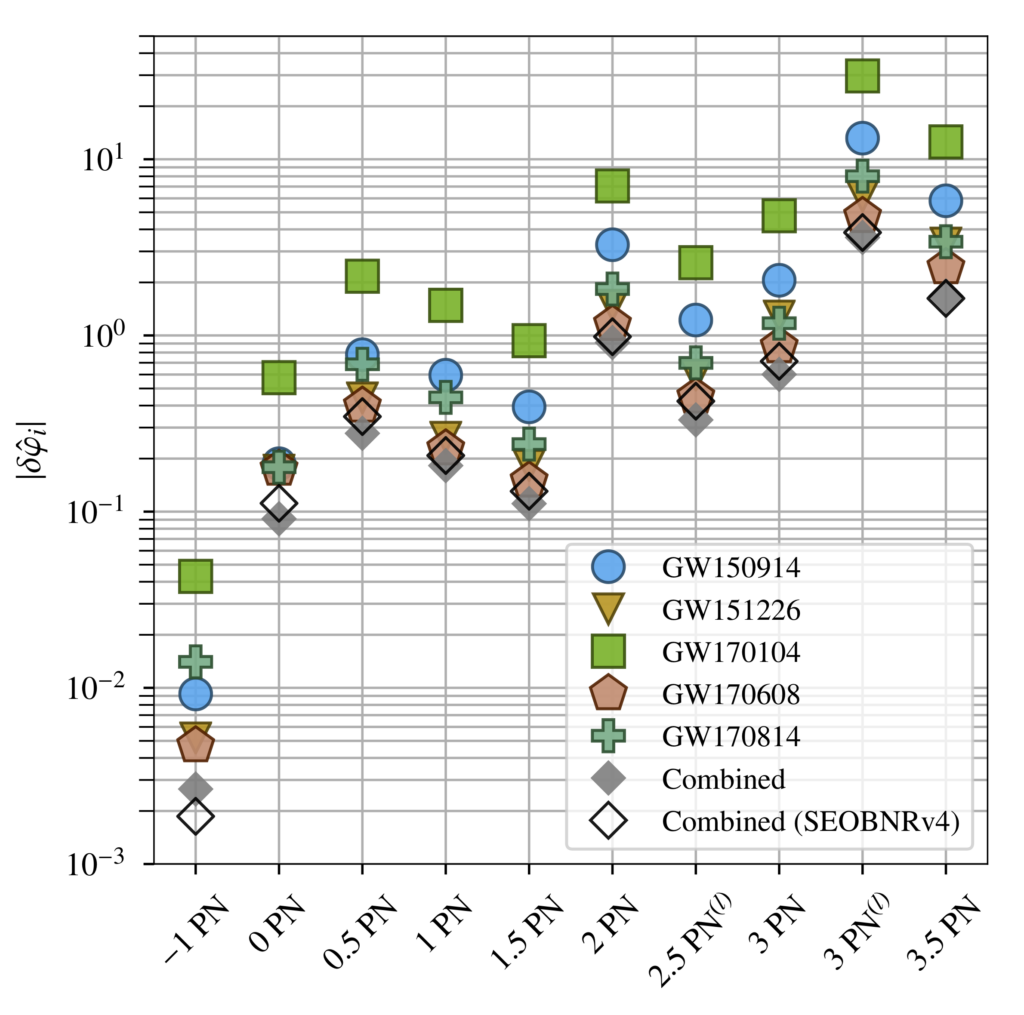
Figure 2: Upper limit on the deviations from the post-Newtonian terms that describe the inspiral stage of a binary merger (Figure 4 of our paper). The -1PN and the 0.5PN terms do not appear in General Relativity, so the upper limit represents the possibility that these terms are present in the data at all. For the other terms, the upper limit indicates a deviation from the General Relativity non-zero value.

A similar analysis is performed on the terms that describe the merger-ringdown stages of the binary, and again we obtain good agreement with the predictions of General Relativity.

The journey of a gravitational wave to our detectors

Not only can we test if General Relativity satisfactorily describes how the source generates gravitational waves (which we did in the previous section by modifying the post-Newtonian and merger-ringdown terms), but also if it accurately describes how the waves travel across the Universe after they have been generated. Some waves, such as water waves, can get dispersed when they travel through a medium, meaning that different frequencies propagate at different speeds and the wave itself gets distorted. Gravitational waves, however, should not be dispersed if General Relativity is correct. By introducing a modification term to the propagation of gravitational waves (accounting for a possible dispersion) and measuring if this modification is present in data, we can constrain alternative theories of gravity that predict a different propagation for gravitational waves.

We describe the deviation from General Relativity by two parameters, A and α, where A gives the magnitude of the deviation and α describes how it depends on the frequency of the gravitational waves. If General Relativity is correct, A should be exactly zero. Different α values correspond to different alternative theories. Figure 3 shows the upper limit on the magnitude of A (which could be positive or negative) for different α values. By combining all the very confident black hole events from the GWTC-1 catalog we obtain our tightest constraints so far on alternatives to General Relativity.

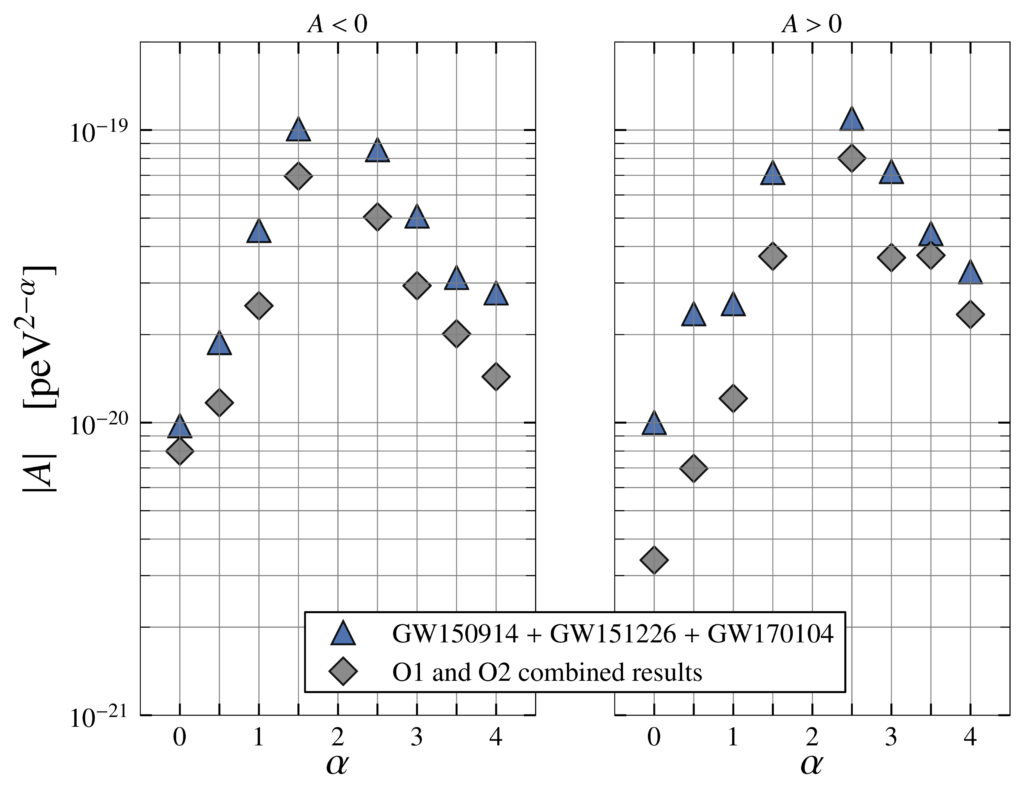
Figure 3: Upper limit on the deviations from the dispersion relation predicted by General Relativity (Figure 5 of our paper). The blue triangles represent updated limits obtained from previously published gravitational waves, and the grey diamonds represent the new constraints from combining the very confident black hole events observed in the first (O1) and second (O2) observing runs of Advanced LIGO and Virgo.

The particular case of α=0 and A>0 corresponds to the propagation effects of a massive graviton as the quantum particle responsible for gravitational waves. In General Relativity the graviton is expected to have no mass, while some alternative theories of gravity predict that the graviton is massive. With gravitational waves we can establish limits on how large the mass of the hypothetical massive graviton can be. Here, we find the limit of the graviton mass to be at maximum 4.7 x 10-23 eV/c2, an improvement of 1.6 with respect to our previous calculation. For comparison, the least massive particles known (that do not have zero mass) are neutrinos: we know that at least two neutrinos have masses greater than 0.009 eV/c2; the lightest neutrino could be massless.

Polarization of gravitational waves

General Relativity predicts that gravitational waves only contain two possible polarization states. However, generic theories of gravity allow for up to six different polarization states. Testing the polarization content of a gravitational-wave signal is not possible with the two LIGO detectors, because of their relative orientations. Gravitational-wave observations in conjunction with Virgo have been crucial to provide the first compelling tests of gravitational-wave polarizations. Results using events that were observed with three gravitational-wave detectors (the two Advanced LIGO detectors and the Advanced Virgo detector) have been published previously for GW170814 and GW170817. While we have now a few additional events that were observed by the three detectors, none of them yield as tight constraints as the neutron star merger (GW170817) due to larger uncertainties in the sky location of the black hole mergers. Still, we find no evidence from the new events that alternative polarizations to those predicted by General Relativity are preferred by the data.

Summary

All of the tests performed here have shown that the black hole mergers observed by Advanced LIGO and Virgo are compatible with the predictions of General Relativity. Furthermore, by combining information from the most confident black hole mergers observed to date, we have improved our previous constraints on possible deviations from General Relativity by factors up to 2.5. The future will bring many more observations of black hole binaries, providing even more information on these measurements. Furthermore, we are developing a variety of new ways of testing General Relativity with these signals. We will continue testing Einstein’s theory!

Find out more: