Since 2015, we have had a new way of studying the Universe by means of the direct detection of gravitational waves (GWs). To date, 90 GW events have been registered by the Advanced LIGO and Advanced Virgo interferometers. These GW signals were emitted by inspiralling and merging binary systems of black holes of various masses, binary systems of neutron stars (NSs), and also mixed binaries, composed of a black hole and a NS. Although in reality the binary systems evolve for millions of years until the components finally merge, in our detectors they appear transient — lasting only on the order of seconds or minutes — because their frequency increases rapidly during the last few orbits of the binary. In addition to these short-duration signals, we expect other types of GW radiation that do not change their frequency so rapidly, and can be observed for months and years. These continuous gravitational waves (CWs) are the main subject of the research presented here.
Among possible astrophysical sources of CWs are rotating non-axisymmetric NSs (an extreme example of a sphere deformed into a non-axisymmetric shape would be an American football or rugby ball). NSs are extremely compact objects — with masses similar to the Sun compressed into a ball of about 10 kilometers in radius — formed in the aftermath of massive stars which undergo supernova explosions at the end of their life. NSs may be rapid rotators, spinning with frequencies up to several hundred times per second. A rotating NS may emit detectable CWs, with a frequency of twice the star’s spin frequency, if it possesses an asymmetry with respect to its rotational axis. According to current theoretical models and previous LIGO–Virgo CW searches, such an asymmetric bulge (sometimes also called a “mountain”, “raised plateau” or deformation on one side of the NS) would be at most just a few centimeters high. The bigger the NS asymmetry is, the stronger GWs it generates. For example, a bulge of a few centimeters corresponds to a deformation of a NS from spherical symmetry — also called the ellipticity — of a few parts per million. Determining a NS ellipticity is not easy, but once detected it will provide a truly unique insight into the properties of the extremely dense matter and strong magnetic fields of which the star is composed. Currently these properties are very poorly known. In addition to about 3000 NSs known to astronomers because they are electromagnetically bright (for example, as radio pulsars), our Galaxy, the Milky Way, is estimated to contain as many as 100 million NSs not visible in electromagnetic radiation because they are either too faint to be detected, or their electromagnetic emission is not directed towards Earth. However, if any of these NSs are sufficiently asymmetric, they may emit GWs detectable by our interferometers. The ultimate goal of our search is to detect GW signals from these millions so far unobserved objects.
Searches like this one have been carried out using the Advanced LIGO and Advanced Virgo data previously, in the O1, O2 and the first half of the O3 (O3a) observing periods. Here we summarize recent results obtained on the most sensitive data up to now, the LIGO–Virgo O3 observing run (April 2019 – March 2020).
Detecting very weak CW signals buried in the detector data is a difficult task. A CW signal is basically periodic, but many factors modify the signals received at the detector. One is the Doppler effect which shifts the signal frequency over time, because our detectors are placed on Earth which is rotating and moving around the Sun. The signal’s frequency is therefore modulated depending on the relative positions of the source and the detector, and on the GW frequency itself. To complicate things further, the GW frequency will evolve in time as well — a NS loses rotational energy through the emission of GWs and in electromagnetic radiation, causing a gradual decrease of the signal frequency called spin-down. We also look for GW signals spinning up (increasing their frequency) to be sure we don’t miss potentially interesting signals with these characteristics. An example of this type of a signal would be an inspiralling binary system of light compact objects, e.g., planetary mass black holes.
For a given sky position, spin frequency and spin-down of the source, we can precisely compute the CW waveform and detect the signal hidden in the data using well-known data analysis techniques, such as the matched filtering method. The real difficulty resides in the fact that the actual astrophysical properties of the CW source are unknown – therefore, we need to go through a large number of possible combinations of parameters, which makes the search computationally challenging. In order to deal with it practically, we have devised multi-step (hierarchical) pipelines, that employ matched filtering on small pieces of data (time segment durations ranging from half an hour to several days), and then combine these partial pieces of information to gather the evidence for the presence of a CW signal with particular parameters in the data. Hierarchical search methods are less sensitive than the optimal procedure, which is a direct application of matched filtering, but they are robust with respect to signal model uncertainties, and practically feasible from the computational point of view, despite the lack of information on signal’s parameters. Another complication is related to the detector data themselves: the data contain, at many frequencies, various instrumental disturbances which may look very much like CW signals. An important part of the analysis is to identify these spurious signals and remove them from the list of GW candidate signals.
The sensitivity reached by the Advanced LIGO and Advanced Virgo detectors during the O3 run, which lasted for about a year, enabled the most sensitive search for unknown CW sources ever done: surveying the whole sky, GW frequencies between 20 Hz and 2048 Hz and a rate at which the frequency changes (spin-down range) from -10-8 Hz/s to 2×10-9 Hz/s. In the current search the results were obtained by four independent hierarchical data-analysis pipelines. The methods covered different frequency and spin-down ranges, used data segments of different lengths, applied different data cleaning procedures to reduce the impact of noise in the data, and used different techniques to follow-up possible GW signal candidates, sometimes employing modern machine learning methods, such as deep neural networks.
Our analyses did not find any statistically significant evidence of CW signals in the LIGO–Virgo O3 data. In order to constrain theoretical models of CW emission, we have computed the upper limits on the GW amplitude: limits on how strong a CW signal could be to still not be detected. The upper limits are presented in Figure 2. These correspond to 95% confidence that no higher signal amplitudes are present in the data. Our best upper limits are a signal amplitude of 1.1×10-25 at the frequency of 111.5 Hz. These results are 1.5 times better — constrain the amplitude to smaller values — than those from the previous observation period, called O2.
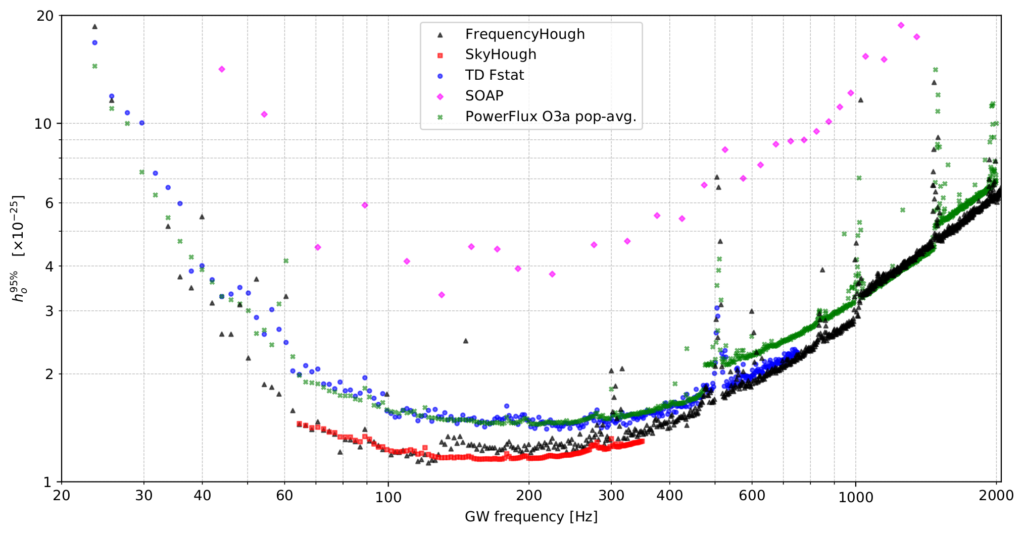
Figure 2: Comparison of 95% confidence upper limits on GW amplitude across a range of frequencies, obtained by the four data-analysis pipelines: FrequencyHough (black triangles), SkyHough (red squares), SOAP (magenta diamonds), and Time-Domain F-statistic (blue circles). Previous LIGO–Virgo search upper limits, obtained with the PowerFlux pipeline on the first part of the O3 run (O3a data) are marked with dark-green crosses (Fig. 15 in the publication).
Figure 3 shows additional astrophysical information we have learned with this search, which is the relation between the frequency, spin-down and distance of a potentially detectable source. For instance, at frequency 200 Hz we would be able to detect a CW signal from a NS within a distance of 100 pc (parsecs) if its ellipticity were at least 3×10−7. Similarly, in the middle frequency range, around 550 Hz, we would be able to detect the CW signal up to a distance of 1 kpc (1000 parsecs), with ellipticity greater than 5 × 10−7. For comparison, the radius of our Galaxy is about 15 kpc. Although no detection can be claimed, our results are nevertheless interesting from the astrophysical point of view and shed more light on the properties of Galactic NSs. Our upper limits are starting to probe the range of ellipticities up to 10−7 – 10−6 for some models of younger NSs in which the deformation is not supported by the elasticity of the crust, but by a non-axisymmetric magnetic field.
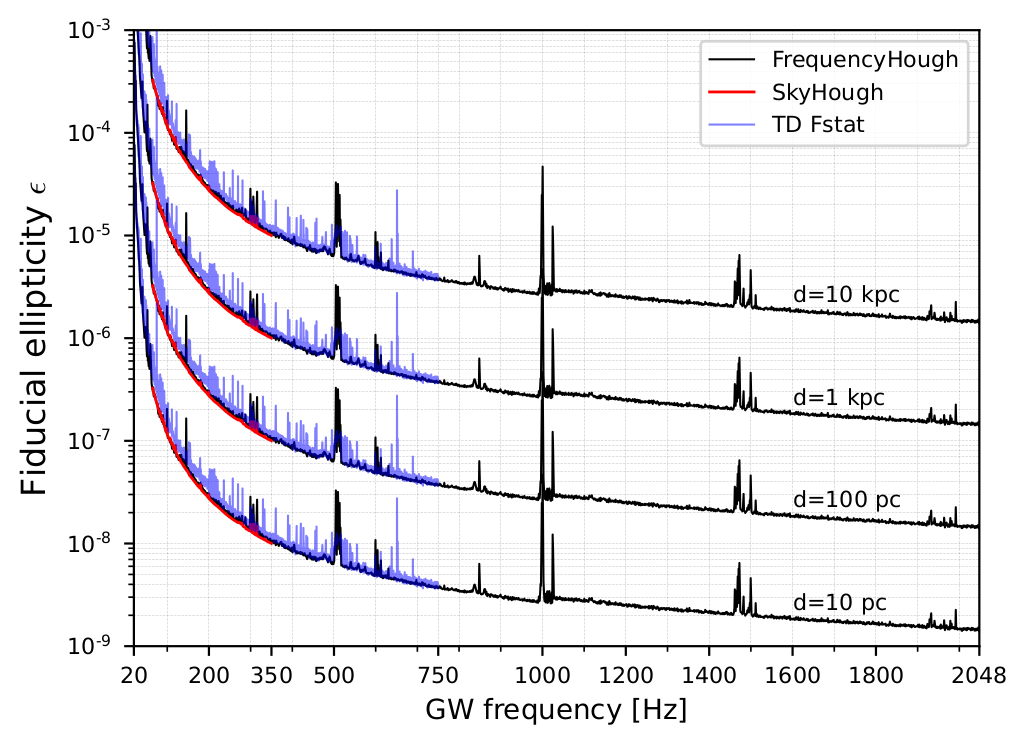
Figure 3: Detectable neutron star ellipticity, as a function of the GW frequency at distances of 10 kpc, 1 kpc, 100 pc, and 10 pc (from top to bottom). Results from the FrequencyHough pipeline are marked in black, from SkyHough in red and from the Time-Domain F-statistic in blue (Left panel in Fig. 16 in the publication).
In addition to constraints on ellipticities of isolated NSs, we show that our results may be used to make statements about the rate and abundance of inspiraling, hypothetical very light black holes (with masses like those of planets and asteroids), which may have been created in the early Universe and may constitute a fraction of the mysterious dark matter. GW signals from binary systems, in which at least one component is a very light black hole, are evolving their frequency very slowly during their inspiral phase — for a long time they are practically CW signals with a small spin-up change in frequency. We show that CW searches may in the near future be used to detect such objects, providing information on light black holes, if they are present in the vicinity of our Solar System.
As the Advanced LIGO and Advanced Virgo detectors increase in sensitivity, and with the help of the KAGRA detector in the world-wide network, we will be able to detect CWs from spinning NSs with even smaller deformations, reach out to a larger portion of the Galaxy, and test various other hypotheses such as the existence of very light black holes. Detecting these signals will open a new frontier in the study of these fascinating compact objects, which will become true laboratories for astrophysics and fundamental physics: once a CW source is detected, it can be monitored, in principle, for arbitrarily long times. This allows us to increase the detection confidence to almost absolute certainty, measure NS parameters with extremely high accuracy, calibrate our detectors and test theories of gravity.
Find out more
- Visit our websites:
- Read a free preprint of the full scientific article here or on arXiv.org


