LIGO and Virgo scientists have been waging a decades-long campaign to find unsightly bulges on neutron stars. Neutron stars are highly compact stars that are created in the collapse of a star heavier than our Sun as the electrons in its atoms combine with the protons to form a ball of mostly neutrons of radius not much greater than 10 km. If they were much more compact, neutron stars would form black holes. Some neutron stars are fast-spinning pulsars which, like lighthouses, emit beams of electromagnetic radiation with extremely regular periods when observed from a fixed vantage point. Their spin frequencies can be so stable as to rival the performance of atomic clocks on Earth.
An asymmetric bulge on a neutron star could create continuous gravitational waves. Imagine, for example, a large, raised plateau with a height of a millimeter or centimeter on one side of the star. As the neutron star and hence such a slight protrusion spins around — tens to hundreds of times per second in the stars that are potentially detectable — it disturbs neighboring space-time, producing gravitational radiation. The frequency of the gravitational waves is then twice the stellar rotational frequency and nearly constant, with only a slight decrease in the frequency with time as the star’s rotational energy loss to gravitational waves leads to spin-down. Moreover, the star’s smooth spin leads to emission of gravitational waves that are continuous in time.
We have been searching for years for such continuous gravitational waves in the hope that each new improvement to the world’s gravitational wave detectors would give a glimpse of the incredibly tiny waves that might be emitted by a bulging neutron star. For reference, the strain amplitude was 10-21 for the very first gravitational wave detection in September 2015. That signal came from a pair of massive black holes 1.3 billion light years away and was detectable for only about two tenths of a second. Continuous gravitational waves would be even weaker, by several orders of magnitude, despite coming from stars only hundreds to thousands of light years away, because the radiated energy is so much smaller.
Using the first six months of data from the most recent LIGO and Virgo Observing Run (O3), we have now probed deeper than ever before in our galaxy to look for previously unknown neutron stars with detectable bulges. The new search looks for isolated stars everywhere in the sky and is able to detect strain amplitudes below 10-25, making it the most probing search of its kind to date, one with sensitivity to extremely tiny bulges.
How tiny is tiny? A neutron star bulge is characterized by its equatorial ellipticity. This number describes how much the star is deformed from a shape that is symmetric about the rotation axis. Now one does expect a fast-spinning neutron star to deviate from a perfect sphere. A circle around its equator should be slightly longer than one going over its pole, because of the same centrifugal effects that slightly flatten the Earth. The resulting polar ellipticity, however, does not generate gravitational waves because as the star spins, there is no change in its gravitational effects on nearby space. There is no “swirling” of space like the one caused by a bulge going around and around. We don’t know precisely what to expect for typical neutron star equatorial ellipticities. Conventional nuclear theory permits a value as high as 10-5, which would correspond to a bulge as high as 10 cm, but even significant bulges that might be present at a neutron star’s birth following a supernova tend to anneal with time, leading to smaller ellipticities. In practice, we expect typical neutron stars to have much lower ellipticities, but are not sure by how much.
One might expect it to be easy to detect a single-frequency continuous-wave signal. The Fast Fourier Transform used widely in signal processing could be applied to the gravitational wave strain data to reveal a “spike” at the right frequency. But a number of complications make it much more challenging than that. First, because the star’s rotation is slowing gradually, one must keep making corrections for the decreasing frequency, and since one doesn’t know a priori how gradual the decline is, one must search for many possibilities. In the most recent all-sky search, dozens of possible spin-down values are tried, which increases the computational cost of the search.
What makes the computational cost far greater, though, is the effect of the Earth’s motion, both from its daily rotation and from its orbital motion around the Sun. One must explicitly correct for the Doppler shift of the apparent frequency of the gravitational wave signal due to the Earth’s motion relative to the star that emits the signal (analogous to the Doppler shift of siren sounds from a fire engine passing by). See Figure 1 for an illustration of the effects on frequency. Unfortunately, the explicit corrections for the rotational and orbital Doppler modulations are different for every point on the sky, which means one must keep making adjustments in the search as one “steps” around the sky in the search. One additional complication is that the signal’s apparent amplitude variation with time depends on the relative orientation of the star’s rotation axis with respect to our line of sight to it. The variation also depends on the orientations of the gravitational wave detectors on the surface of the Earth (latitude, longitude and compass directions of the interferometer arms) — and we don’t know the stellar orientation!
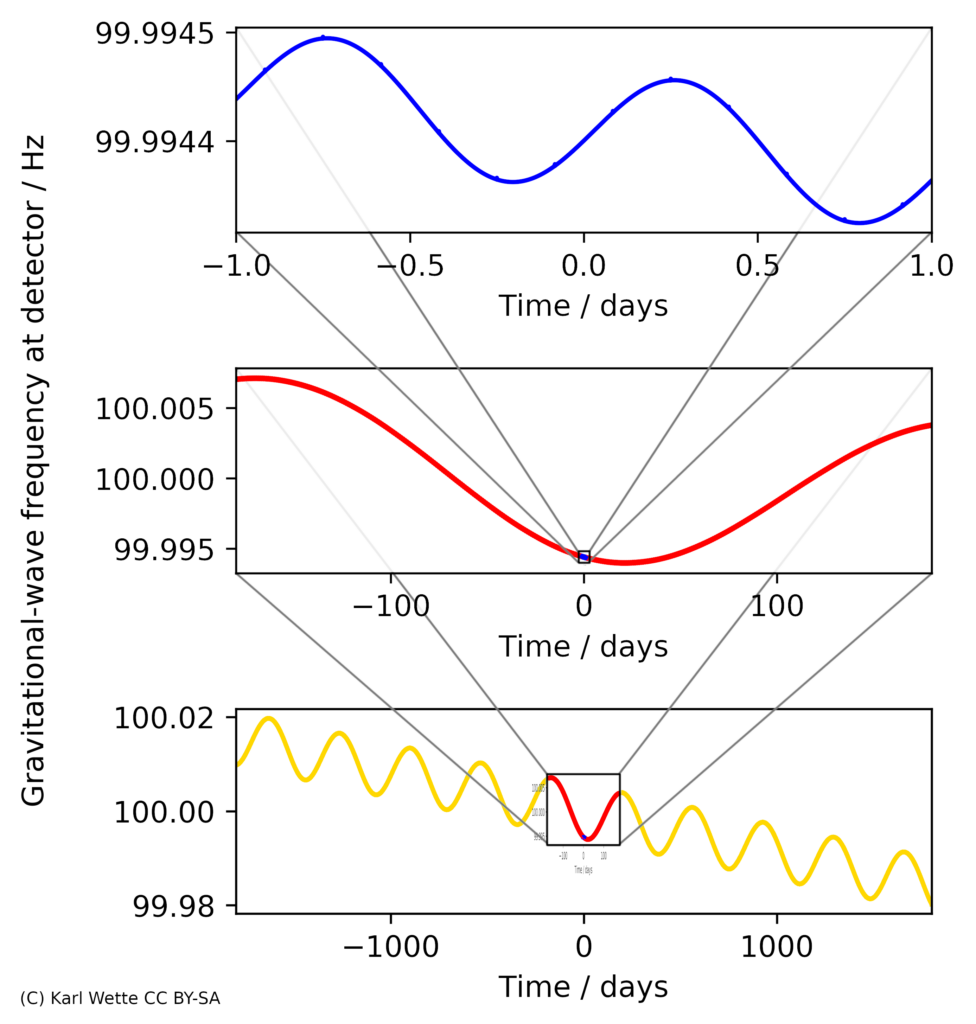
Figure 1: Long-term frequency evolution of a continuous gravitational-wave signal. Over short times, the signal from a Galactic neutron star will look almost perfectly constant in both frequency and amplitude. However, over longer durations, the frequency of the signal will slowly change, for two reasons. The first reason is that, as the neutron star emits gravitational and electromagnetic waves, it loses energy which causes it to rotate more slowly. The second reason is that the detector here on Earth is moving with respect to the neutron star, which changes the frequency of the gravitational waves observed in the detector. (Credit: K. Wette)
Taking all of these corrections into account vastly increases the computational cost over that of a simple Fourier transform, despite making compromises in achievable strain sensitivity by segmenting the data. In the recent search, more than 15 million CPU hours were consumed over nearly a year using computers hosted by LIGO Laboratory and using other computers available globally on the Open Science Grid.
After searching through the first six months of the O3 data and identifying more than 140,000 potentially candidates in frequency, spin-down and sky location, we followed these outliers with an even deeper search in multiple stages, including a final-stage search in the full 11-month O3 data set for a small number of residual candidates. In the end, no outlier survived the follow-up: this means that no continuous GWs have been observed, and therefore we can give only upper limits on signal strength.
One way to characterize the sensitivity of the search is via the range in kiloparsecs (kpc) to which we could have seen a signal from a neutron star of a particular ellipticity. Figure 2 shows the range sensitivity using the initial O3 data, with respect to the frequency of the gravitational waves. Stars with larger ellipticities emit stronger gravitational waves and hence can be seen farther away.
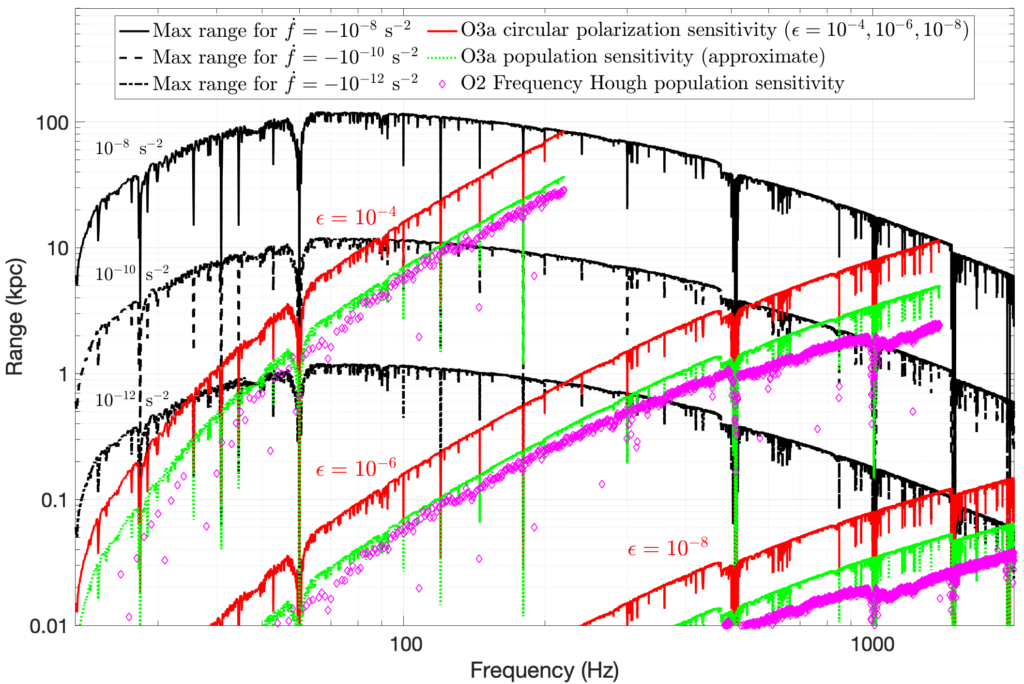
Figure 2: Ranges (in kpc) of the search for neutron stars spinning down solely due to gravitational radiation; the frequency of the gravitational radiation (in Hz) is shown on the horizontal axis. The three black curves (solid, dashed, dot-dashed) that peak below 100 Hz represent the maximum possible ranges under the assumption that the maximum rate ḟ at which the neutron star slows down (i.e., the maximum spin-down magnitude) is (10-8, 10-10, 10-12) per second squared, for the three curves respectively. The three sets of three colored curves (red solid, green dotted, magenta diamonds) that generally rise with frequency are the ranges for which the upper limits apply for three different assumed equatorial ellipticities of ε = 10-4, 10-6 and 10-8. The dotted curves correspond to the best (red) and typical (green) results obtained here with the O3 data while the magenta diamond curves show the typical results obtained by a previous search, which used data from the second observing run (O2): the difference in the curves shows the improved sensitivity of the present search, which could observe neutron stars with a given ellipticity at larger ranges, i.e., farther away.
The sensitivity of the latest search is greatly improved over previous all-sky searches of comparable breadth in frequency and spin-down, especially at higher frequencies. The improvement comes in large part from the implementation of “quantum squeezing” in the LIGO interferometers, a clever technique to gain more sensitivity for a fixed laser intensity. Additional searches will be carried out in the full-O3 data using complementary search methods, to dig still deeper in the noise, and further gains in sensitivity are expected from the future O4 and O5 observing runs, following further detector improvements. We expect future searches to extend further into our galaxy for any given ellipticity, steadily increasing the chances for discovery.
Find out more:
- Visit our websites:
- Read a free preprint of the full scientific article here or on arxiv.org.
- Read an introduction to continuous gravitational waves here.

