Gravitational waves (GWs) from binary black hole and binary neutron star systems have been responsible for the new discoveries made with gravitational-wave detectors. But inspiraling binaries are not the only way to make GWs: other promising sources include rotating neutron stars. These objects are known to rotate rapidly but are slowing down over time, due in part to GW emission. This so-called spin-down is extremely small, so that the star’s rotational frequency is almost constant. We therefore refer to these GWs as “continuous-wave” signals: the GWs are emitted continuously, and are at an almost constant frequency. Stringent upper limits have already been placed on the GW amplitude from rapidly rotating neutron stars in previous runs. An artist’s impression of a neutron star is shown in figure 1.
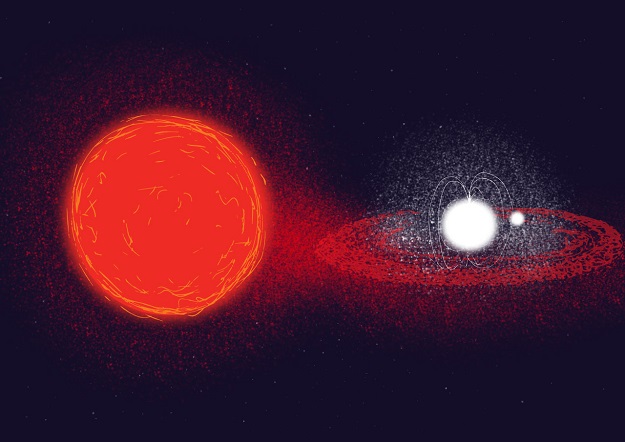
Figure 1: This is an artist’s impression of millisecond pulsar PSR J1023+0038 (white object on the right with magnetic field lines). It extracts matter from its companion star (red object on the left) via an accretion disk (also shown in red). Credit: European Space Agency (ESA).
Pulsars are spinning neutron stars, and are great clocks: we see their radio and X-ray pulses arrive with astonishing regularity, and can measure the arrival times of these pulses with high precision, which means that we can monitor their spin precisely. However, what we do not completely understand are the physical mechanisms responsible for changes in their frequencies and spin-downs, which cause small deviations in the regular arrival times of pulses. GWs can help explain these changes.
To generate GWs, a pulsar needs to be asymmetric around its rotational axis. This asymmetry could be as simple as a “mountain” jutting out from its surface. There are many possible causes for such distortions: they could be “frozen” into the crust or core of the star after the neutron star was born in a supernova, they could be formed from material falling onto the star, or be produced and maintained through extremely large magnetic forces. The GWs could be generated at once or twice the star’s rotation frequency, depending on the cause of emission. The first case occurs if the star wobbles as it spins, or has a superconducting core that is not completely locked to the star’s crust, causing its respective internal density distribution to be misaligned; the second case is caused by any asymmetric distortion.
Our GW searches do not rely on a particular formation mechanism. Rather, they try to measure any kind of continuous signal and later attribute it to a specific process. Because of astronomers’ observations of radio waves, X-rays, and gamma rays, we know the sky position, frequency, spin-down and even the rate of change of spin-down for many pulsars, which greatly helps in the search for a GW signal. For these pulsars, one important goal is to surpass their “spin-down limits”; that is, to be able to measure an amplitude of a GW that is smaller than that predicted by assuming that all of the neutron star’s rotational slow down is being converted to GWs. Once a search reaches this sensitivity level, we are probing a physical plausible emission mechanism, and actually have a chance to detect GWs.
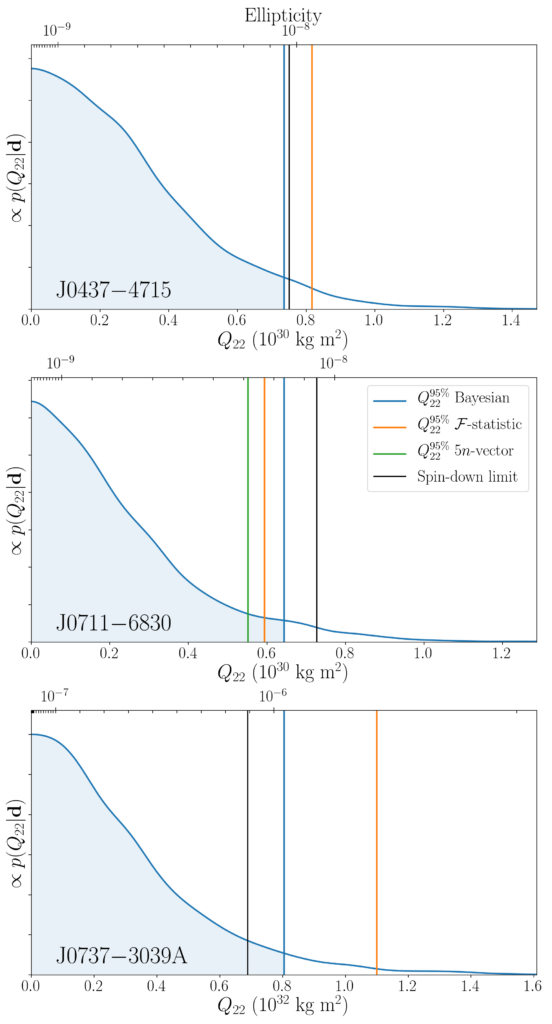
Figure 2 (Fig. 2 from the paper): Constraints on the mass quadrupole moment Q22 and ellipticity (the level of deformation) of three recycled pulsars, based on these new observations. The curves are Bayesian posterior distributions, so the area under the curve between two values of quadrupole moment is the probability that the true value lies within that range, given the data and the assumptions of the model. The black vertical lines represent the spin-down limits for each pulsar, and the colored vertical lines correspond to the 95% degree of belief that the quadrupole moment or ellipticity is below a certain value. When the upper limit measurements (colored vertical lines) of the quadrupole moment (or ellipticity) lie to the left of the black lines, we say that the spin-down limit has been surpassed. For pulsar J0711–6830, located around 358 light years away, the distortion from a perfectly spherical equator has been constrained to be less than the width of a human hair!
The current work uses data from the first, second and third observation runs with the Advanced LIGO and Virgo detectors to place constraints on the GW emission from five pulsars, assuming that the GW emission is either at once or twice the rotational frequency of each star. Although we have not detected any signals, we have a sensitivity that allows us to look below the spin-down limit of two of these pulsars for the first time. It is noteworthy that these are “millisecond pulsars”, meaning they spin very rapidly. And since GW emission becomes more efficient at higher frequencies, these rapidly spinning neutron stars do not require large deformations to produce detectable GWs. Indeed, we find that the equator of the pulsar J0711–6830, located around 358 light years away, is not distorted from a perfect circle by more than the width of a human hair! These upper limits can be seen in more detail in figures 2 and 3. For slower pulsars, such as Crab and Vela, more significant deformations are necessary to generate detectable signals. Small deformations are more likely to form and survive the neutron star’s extremely strong gravity than are larger deformations, so surpassing the spin-down limit for these millisecond pulsars is a very important moment in GW astrophysics.
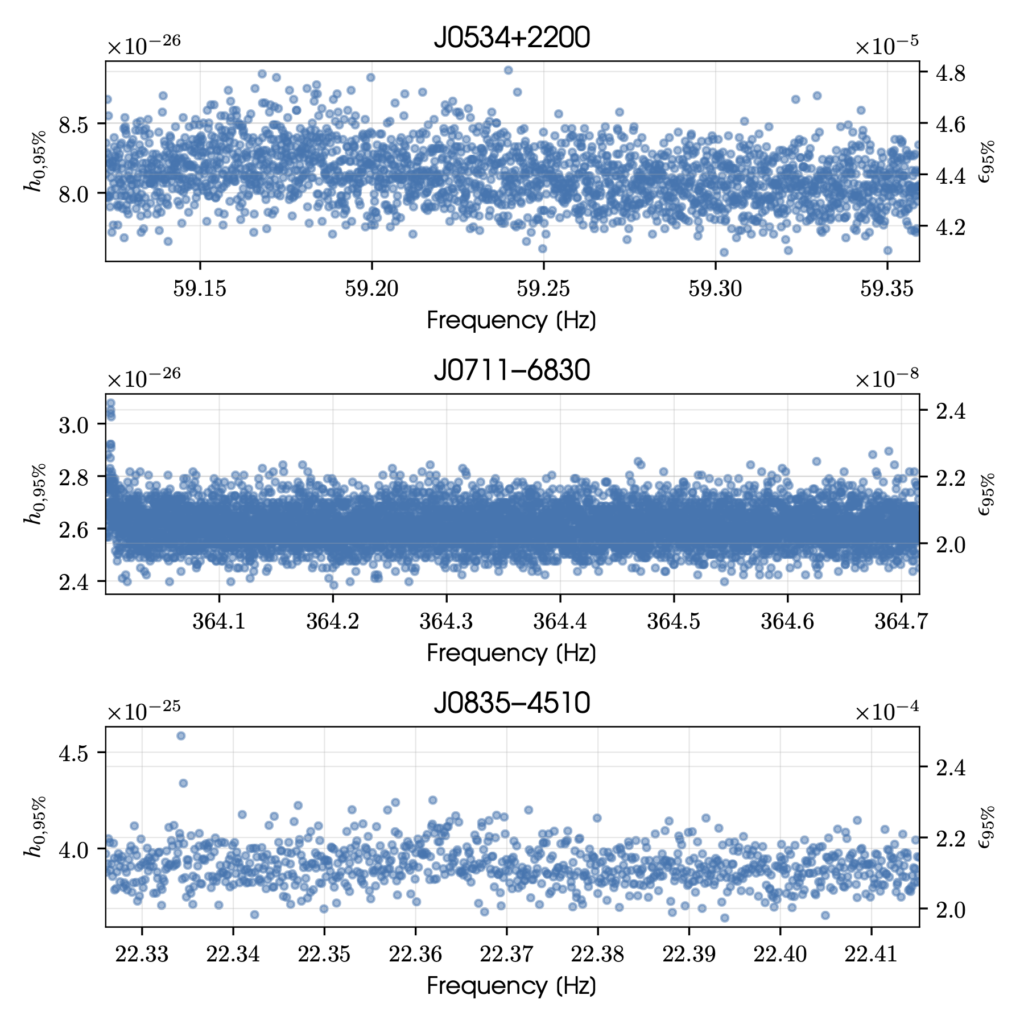
Figure 3 (Fig. 6 from the paper): The 95% confidence level upper limits on the gravitational-wave amplitude h0 and ellipticity ε for the three pulsars analysed in the narrowband analysis. From top to bottom, the upper limits are shown for Crab, the millisecond pulsar for which the spin-down limit was surpassed, and Vela.
Find out more:
- Visit our websites: ligo.org, www.virgo-gw.eu
- Read a free preprint of the full scientific article here. or on arXiv.org.
- Read a nice overview article on pulsars by Michael Kramer (PDF file, 1.2 MB).
- Visit NASA’s “Imagine the Universe!” page on pulsars.

