Testing general relativity with gravitational waves from the first half of the LIGO-Virgo 3rd observing run

Before the detection of gravitational waves from black hole mergers, Einstein’s century-old theory of General Relativity had not yet faced its most stringent tests, tests not possible in either the laboratory or even the solar system. Black hole mergers create some of the strongest, most dynamical gravitational fields allowed by general relativity. The black-hole-merger observations verified two predictions of the theory – gravitational waves can be directly detected and merging black holes exist – but were these the gravitational waves and black holes predicted by Einstein or something close but still different? What can we learn from the gravitational waves that carry the imprint of the violent cataclysm that produced them?

LIGO and Virgo performed novel tests of general relativity for all previous detections as described in the catalog, GWTC-1, and for single events GW190425, GW190412, GW190814, and GW190521. So far, Einstein has passed! But we now have many more black hole mergers to study using the new Gravitational-Wave Transient Catalog 2 (GWTC-2). While we perform several of the same tests as in GWTC-1, we analyze more than twice as many new events as were listed there, and also perform some new tests.

To search for differences from general relativity, we assume some deviation from the theory, such as extra terms in an equation or parameters that can have values different from those in general relativity, to see if that assumption yields a better model for the data. We use signal processing methods with statistical analysis. We end up with some statistical measure of the data and compare that to the expectation from general relativity. Differences could originate from three places: (1) This data is noisy, so we always measure the gravitational wave signal plus the detector noise. (2) In most cases, we make approximations to determine what signal to expect from general relativity and these approximations may not be close enough to the true behavior for some events. (3) The theory of general relativity might not be perfect, and could need to be corrected for such extreme objects as binary black holes. In practice, this means that we cannot easily conclude that a discrepancy lies with general relativity because noise and approximation errors cloud the picture. But we can test if what we find is compatible with general relativity. And that’s what we have done.

As described in our previous paper analyzing GWTC-1, some events don’t match well on to some tests – but we now have more events from which to choose. Whether or not we detect a black hole merger depends on the match of its frequencies to those where the detectors are sensitive. Heavier black holes merge at lower orbital frequencies translating to lower gravitational-wave frequencies. These frequencies are lowered even further (redshifted) during their travel time to Earth by expansion of the Universe. So depending on the frequency, an event might not be suitable for all tests.

Comparing Parts Of The Gravitational Wave Signal To Expectations From General Relativity

General relativity lays down the law on what a black hole must be – namely, an astrophysical black hole has a mass and a spin. Anything else you want to say about black holes is determined by the mass and the spin. If you have two black holes orbiting each other, you have a mass and spin for each. In addition, you have the way the spin axes point and how far apart the black holes are. Starting that way fixes what follows. The initial arrangement evolves by losing gravitational-wave energy, continually shrinking the orbit while orbiting ever faster. This is the inspiral. Then the two black holes merge to become one with its own mass and spin. But this final black hole forms with a distorted shape. General relativity says this distortion produces gravitational waves that carry the distortion away leaving behind just mass and spin. We can test this picture because the initial inspiraling black holes encode the final black hole they become. Furthermore, the details of the disappearance of the distortion (called the ringdown) are also fixed by general relativity.

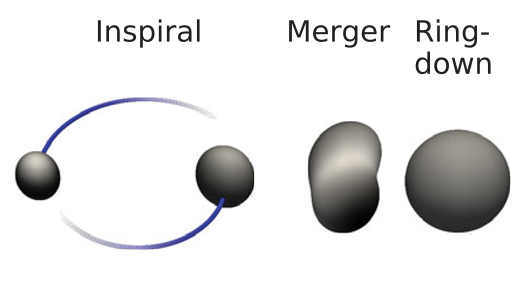
Figure 1: Representation of the three stages of a binary black hole collision: inspiral, merger and ringdown. Adapted from Fig. 2 of the original GW150914 discovery paper.

If the inspiral and ringdown parts of the gravitational wave signal are comparable in strength so we can analyze them separately, we can ask if the one predicts the other. According to general relativity, if you have the details of the inspiral you should be able to infer the ringdown. Do they match? While the noise and limits of the approximations make the comparison imprecise, we find compatibility with general relativity. See Fig. 2 for the results. The distorted merged black hole behaves somewhat like a struck bell. If you strike a bell, you hear a combination of pure tones – the bell’s resonant frequencies. But in a short time that is characteristic of the bell, the notes die out – they are damped. In a similar way, general relativity requires the black hole ringdown to exhibit particular frequencies and damping times. We can then compare the observed properties of the ringdown of the distorted black hole to the ones we predict from the event’s inspiral. While the accuracy is not very good as yet (we hope for better with future detections), the results are compatible with general relativity.

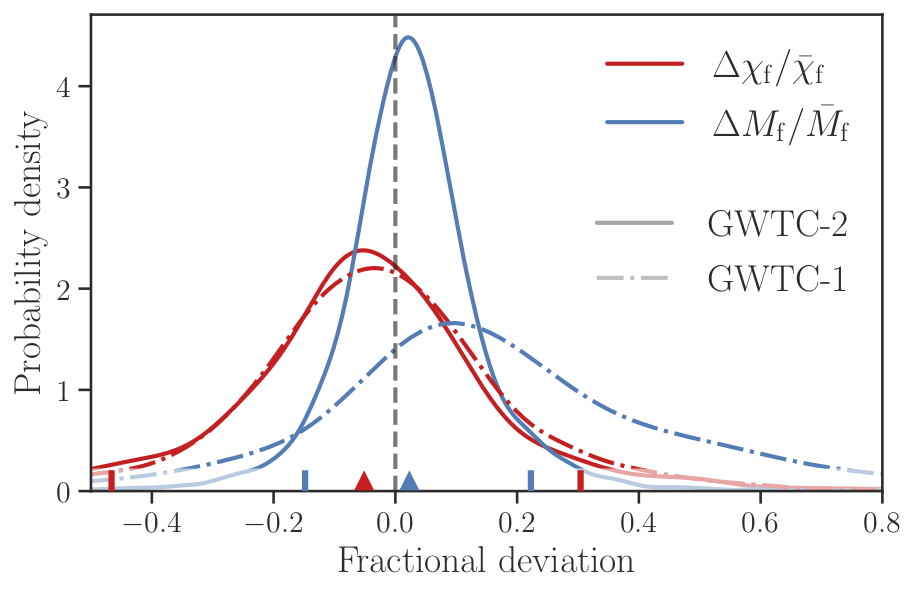
Figure 2: The difference of the final black hole mass Mf (blue) and spin χf (red) inferred from measuring the pre-merger values compared to measuring the post-merger values. The solid lines show the comparison from GWTC-2 and the dot-dash lines from GWTC-1. The vertical, dashed line is the value expected from general relativity. We notice that the newer mass comparison has improved greatly in its closeness to the general relativity value while the spin comparison has not changed much. (Fig. 4 of our paper.)

Are Some Apparent Black Holes Really Mimickers?

The black hole merger produces a huge amount of gravitational radiation, in many cases temporarily outshining the rest of the Universe. What if this radiation came from something that appeared to be a general relativity black hole but really was something else – a black hole mimicker. Several types of mimickers have been proposed. They have the large mass in a small volume of a true black hole but something about them is different. The mimickers fail to have the precise tight connection where how everything depends on mass and spin, as predicted for a general relativistic black hole. For example, the well known one-way character of the black hole’s event horizon may be different for a mimicker. In some proposed mimickers, a mirror-like surface replaces the event horizon. Gravitational waves that would normally go down the black hole end up bouncing back to us creating echoes of the original signal (see Fig. 3 for how this might appear). We find no viable evidence for these echoes.

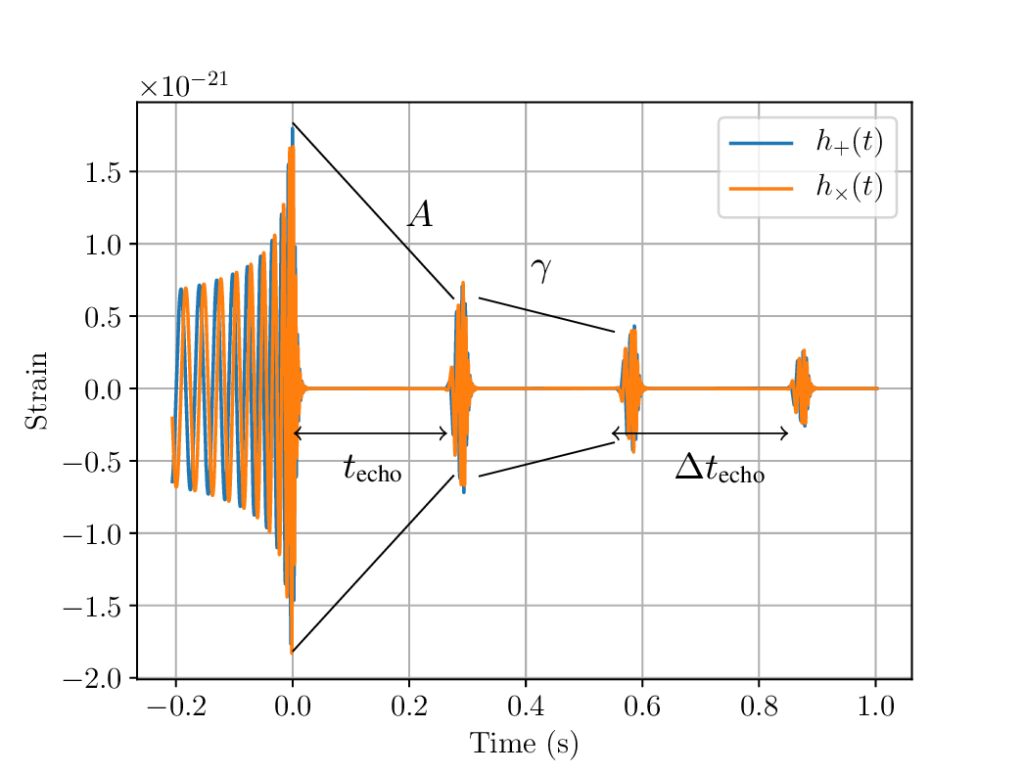
Figure 3: A possible scenario for echoes from a black hole mimicker. As time evolves to the right in the figure, we see the original gravitational-wave signal along with a series of distorted copies of it as the waves bounce back to us from the mimicker’s mirror-like surface. (Courtesy R.K.L. Lo.)

But general relativity might fail for a different sort of mimicker. In these, the event horizon exists but the shape of the black-hole-like object is wrong. We know that spinning objects have a flattened shape. This is true for the Earth and is obvious for the planet Jupiter as viewed through even a small telescope. This flattening can involve gravity even when general relativity is not important. When the spinning object is a black hole, the flattened shape depends precisely on the black hole’s mass and spin. This need not be true for a mimicker which can have a different shape. We examined many black hole mergers for this difference. Nothing significant was found.

Gravitational Waves Take A Long Time To Reach Us From The Merger

A rainbow’s colors hide in sunlight and are revealed when a raindrop disperses the light. Can space-time reveal the “colors” (i.e., frequencies) in gravitational waves? General relativity says not. But, other theories allow a massive graviton that could lead to a dispersion of gravitational waves. We observe gravitational waves that have been traveling to us for billions of years. If gravitons have a mass, they have a lot of opportunity to build up a dispersion. This means that we can detect the imprint of even a very tiny graviton mass. We can also try to amplify any graviton-mass effect that might lurk in the data by combining information from all the events. From our most recent data, we conclude that if the mass were larger than 1.76×10-23 eV/c2, we would find it. We don’t, so the graviton mass is at least that small. We have improved our previous best limit by a factor of 2.7. We point out for comparison that certain types of neutrinos, which have the smallest non-zero masses we know about, have masses of at least 0.009 eV/c2. We also point out that our limit on the graviton mass will further restrict any speculative theories of gravity that have such a mass built in.

Summary

So what’s the answer? Was Einstein right? Is general relativity the correct theory of gravity? We have tested our measurements against the theory with the newly found black hole mergers and, for new types of tests, with already known events as well. In most cases, we can combine the results from different events to strengthen our conclusions. The bottom line is that, when we take noise and inaccurate approximations into account, everything we found is compatible with general relativity. As we show in the figures, some of our tests do not yield very strong results. In the future, we expect to detect many more black hole mergers to help us give a more definitive answer.

Find out more: