Recent progress in generating quantum states of squeezed vacuum has made it possible to enhance the sensitivity of the 4 km gravitational wave detector at the LIGO Hanford Observatory to an unprecedented level. LIGO, the Laser Interferometer Gravitational-wave Observatory, operates large Michelson interferometers with the goal of detecting gravitational waves from black holes, neutron stars, supernovae, and remnants of the Big Bang. Albert Einstein predicted the existence of gravitational waves as part of his general relativity theory. They are extremely faint and instruments with exquisite sensitivity are required to detect them. For example, two binary neutron stars, which are spiraling into each other, and located in the Virgo galaxy cluster will produce a signal no bigger than one thousandth of a proton radius.
The Heisenberg uncertainty principle states that we can’t know both the position and the velocity of a quantum particle perfectly–the better we know the position, the worse we know the velocity, and vice versa. For light waves, the Heisenberg principle tells us that there are unavoidable uncertainties in amplitude and phase that are connected in a similar way. One of the stranger consequences of quantum theory is that there must be fluctuating electric and magnetic fields, even in a total vacuum. In a normal vacuum state, these “zero-point” fluctuations are completely random and the total uncertainty is distributed equally between the amplitude and the phase. However, by using a crystal with non-linear optical properties, it is possible to prepare a special state of light where most of the uncertainty is concentrated in only one of the two variables. Such a crystal can convert normal vacuum to “squeezed vacuum“, which has phase fluctuations SMALLER than normal vacuum! At the same time, the amplitude fluctuations are larger, but phase noise is what really matters for LIGO.

Sheila Dwyer and Alexander Khalaidovski testing the squeezed vacuum source optics inside a “portable clean room” (plastic curtains pulled aside temporarily for the photo). Dwyer was a grad student at MIT, and is now a postdoc at LIGO Hanford Observatory. Khalaidovski was a grad student at the Albert-Einstein-Institut in Hannover, Germany, and is now a postdoc at the Institute for Cosmic Ray Research at the University of Tokyo.
During the last observational run in 2009 and 2010, the LIGO gravitational wave detectors were limited by zero-point fluctuations over most of their frequency range. In 2011, a squeezing crystal and associated precision optics and controls were installed at the LIGO Hanford Observatory to test the idea of reducing the vacuum phase fluctuations. Squeezed vacuum was directed into the output of the large Michelson interferometer. As predicted, this was found to reduce the noise at frequencies above 200 Hz by a small but significant amount, as shown in the figure below. During that test, the LIGO Hanford interferometer achieved better sensitivity than any gravitational wave detector operated to date. This experiment was an important step, following excellent earlier results achieved at higher frequencies with the GEO600 detector in Germany, and shows how future gravitational wave detectors can be made even more sensitive by manipulating the quantum properties of light.
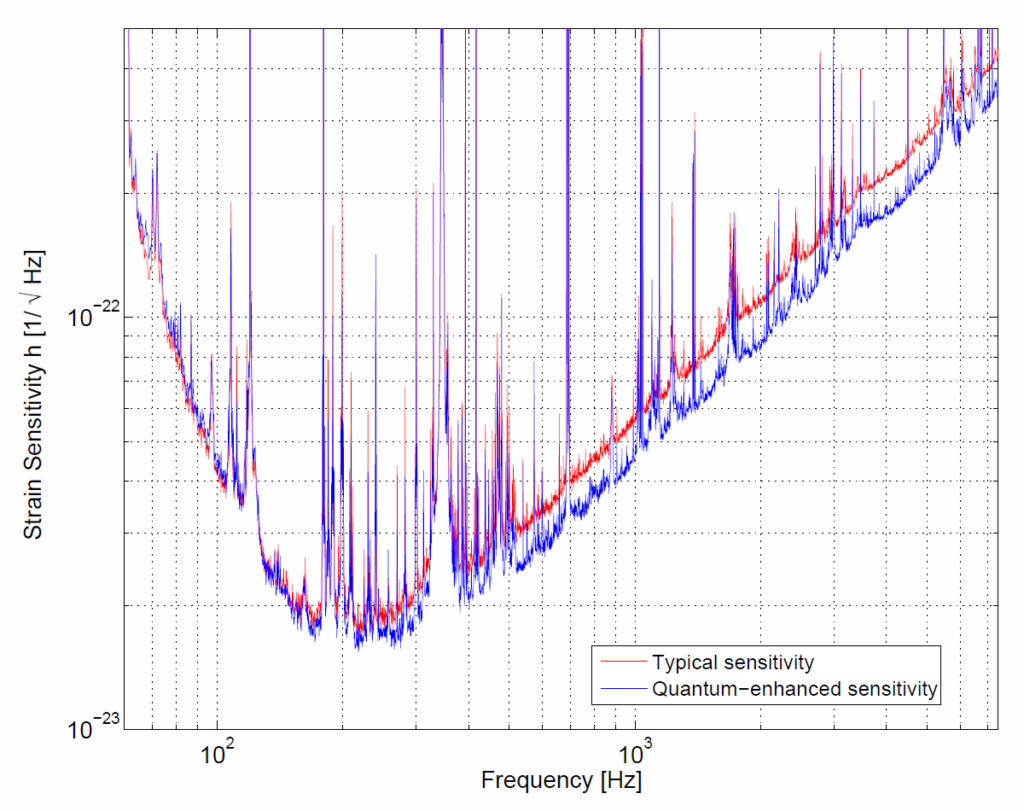
Measured improvement in the sensitivity of the LIGO Hanford gravitational wave detector from this study. The vertical axis indicates the detector noise level as a function of frequency, so the blue curve (“quantum-enhanced” using squeezed vacuum) is better (lower) than the red curve at frequencies above ~200 Hz.
Since LIGO is currently in the middle of an ambitious upgrade–the Advanced LIGO project–the detector used in this experiment has been decommissioned. The Advanced LIGO design was set long before the current squeezed vacuum experiment. As a result, quantum enhancement technologies are currently not in its base plan. However, they are ready to be included in the first upgrades. The successful demonstration of squeezed vacuum technology offers another way for these detectors to become more sensitive and thereby reach out even farther into the Universe.

Sheon Chua with the squeezed vacuum source installed beside the interferometer at LIGO Hanford Observatory. Chua was a grad student at the Australian National University, and is now a postdoc there.
S. Dwyer, S. Chua, L. Barsotti and D. Sigg were the leading scientists on this experiment, but a number of LIGO Scientific Collaboration members contributed directly to its success. M. Stefszky, A. Khalaidovski, M. Factourovich and C. Mow-Lowry assisted with the development of the squeezed vacuum source under the leadership of N. Mavalvala, D. McClelland and R. Schnabel. K. Kawabe supervised the integration of the squeezed vacuum source into the LIGO interferometer, with invaluable support from M. Landry and the LIGO Hanford Observatory staff. N. Smith-Lefebvre, M. Evans, R. Schofield and C. Vorvick kept the LIGO interferometer at its peak sensitivity and supported the integration of the squeezed vacuum source, with contributions from G. Meadors and D. Gustafson.
Read more:
- Paper published in Nature Photonics: Enhanced sensitivity of the LIGO gravitational wave detector by using squeezed states of light (online access may require subscription)
- Overview of the Advanced LIGO project
- Wikipedia entry on squeezed light
- GEO600 squeezed light demonstration (2011)

